2022-2023学年福建省福州市八县(市、区)一中高二(下)期中数学试卷
发布:2024/8/27 2:0:8
一、单项选择题(本大题共7小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.已知抛物线C:y2=2x上一点到y轴的距离是3,则该点到抛物线C焦点的距离是( )
组卷:360引用:4难度:0.9 -
2.已知随机变量X的分布列为
,2,3,4,5),则P(2≤X<5)=( )P(X=i)=ia(i=1组卷:273引用:7难度:0.8 -
3.将5个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
组卷:319引用:6难度:0.7 -
4.已知某地市场上供应的一种电子产品中,甲厂产品占
,乙厂产品占12,丙厂产品占14,甲厂产品的合格率是95%,乙厂产品的合格率是90%,丙厂产品的合格率是90%,则从该地市场上买到一个产品,此产品是次品的概率是( )14组卷:352引用:3难度:0.7 -
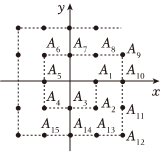 5.如下图,在平面直角坐标系中的一系列格点Ai(xi,yi),其中i=1,2,3,⋯,n,⋯且xi,yi∈Z.记an=xn+yn,如A1(1,0)记为a1=1,A2(1,-1)记为a2=0,A3(0,-1)记为a3=-1,⋯,以此类推;设数列{an}的前n项和为Sn,则S80=( )组卷:64引用:4难度:0.5
5.如下图,在平面直角坐标系中的一系列格点Ai(xi,yi),其中i=1,2,3,⋯,n,⋯且xi,yi∈Z.记an=xn+yn,如A1(1,0)记为a1=1,A2(1,-1)记为a2=0,A3(0,-1)记为a3=-1,⋯,以此类推;设数列{an}的前n项和为Sn,则S80=( )组卷:64引用:4难度:0.5 -
6.已知双曲线
的左右两个顶点分别为A、B,点M1,M2,⋯,Mn为双曲线右支上的n个点,N1,N2,⋯,Nn分别与M1,M2,⋯,Mn关于原点对称,则直线AM1,AM2,⋯,AMn,AN1,AN2,⋯,ANnC:x23-y2=1
这2n条直线的斜率乘积为( )组卷:73引用:4难度:0.6 -
7.若对任意的x1,x2∈(0,m),且x1<x2,都有
<1成立,则实数m的最大值是( )x1lnx2-x2lnx1x1-x2组卷:189引用:5难度:0.5
四、解答题(本大题6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
-
20.已知椭圆C:
过点x2a2+y2b2=1(a>b>0),且离心率为(0,3),设A、B分别为椭圆的左右顶点,F1、F2为椭圆的左右焦点,点P为椭圆C上不同于A、B的任意一点,点Q是椭圆C长轴上的不同于A、B的任意一点.12
(1)求椭圆C的标准方程;
(2)当△PF1F2内切圆的面积最大时,求内切圆圆心的坐标;
(3)设直线PQ与椭圆C的另一个交点为点N,若的值为定值,则称此时的点Q为“稳定点”,问:是否存在这样的稳定点?若有,试求出所有“稳定点”,并说明理由;若没有,也请说明理由.1|PQ|+1|QN|组卷:71引用:3难度:0.5 -
21.已知函数
.f(x)=(x-1x)-klnx,k>0
(1)若对∀x∈(0,1),f(x)<0恒成立,求k的取值范围;
(2)求证:对∀x∈(0,1),不等式恒成立.exx2+2<x2-1xlnx组卷:72引用:3难度:0.4


