当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省长沙市开福区立信中学八年级（上）期中数学试卷

发布：2024/9/22 16:0:8

一、选择题（本大题共10小题，每小题3分，共30分）

1．在一些汉字的美术字中，有的是轴对称图形．下面四个美术字中可以看作轴对称图形的是（　　）
A． B． C． D．
组卷：1265引用：58难度：0.9
解析
2．按照知情同意自愿的原则，我国正积极引导3岁至11岁适龄无禁忌人群“应接尽接”，截至10月29日，该人群已接种新冠疫苗超过353万剂次，则353万用科学记数法表示为（　　）
A．3.53×10⁵ B．35.3×10⁴ C．0.353×10⁷ D．3.53×10⁶
组卷：119引用：3难度：0.8
解析

3．要调查下列问题，适合采用抽样调查的是（　　）

A．疫情期间，了解全校师生入校时体温情况

B．检测我国研制的C919大飞机的零件的质量

C．了解一批灯泡的使用寿命

D．了解小明某周每天参加体育运动的时间

组卷：863引用：8难度：0.8

解析

4．一个等腰三角形的两边长分别为2，4，则它的周长为（　　）
A．8 B．10 C．9 D．8或10
组卷：1098引用：9难度：0.5
解析
5．某市要在河流l上修建一个水站P，向居民区A，B提供自来水，要使点P到A，B的距离之和最短，则下列确定点P位置的作法正确的是（　　）
A． B．
C． D．
组卷：143引用：3难度：0.5
解析
6．下列条件不能得到等边三角形的是（　　）
A．有两个内角是60°的三角形
B．有一个角是60°的等腰三角形
C．腰和底相等的等腰三角形
D．有两个角相等的等腰三角形
组卷：1595引用：16难度：0.5
解析
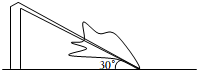7．如图，一棵大树在一次强台风中于离地面5米处折断倒下，倒下部分与地面成30°夹角，这棵大树在折断前的高度为（　　）
A．10米 B．15米 C．25米 D．30米
组卷：844引用：11难度：0.5
解析
8．已知，a=3⁴⁴，b=4³³，c=5²²，则a,b,c的大小关系是（　　）
A．a＞b＞c B．a＞c＞b C．a＜b＜c D．b＞c＞a
组卷：1144引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共9小题，分值分别为6，6，6，8，8，9，9，10，10，共72分）

24．“整体思想”是中学数学解题中的一种重要的思想方法，它在代数式的化简与求值问题中应用极为广泛，例如：已知2a-b=1，在求多项式2024-6a+3b的值时，我们常常将多项式2024-6a+3b写成2024-3（2a-b）的形式，再将2a-b=1代入即可得到2024-3（2a-b）=2024-3=2021．请同学们尝试利用“整体思想”解决下列问题：
（1）已知2a+3b-4=0，求代数式4^a•8^b的值；
（2）已知x²-3x+1=0，求代数式x³-2x²-2x+3的值；
（3）若关于x的多项式（x²+nx-2）（x²-mx+1）化简后的结果中x³项的系数为1，若a-b=m,a-c=n,求代数式a²+b²+c²-ab-ac-bc的最小值．
组卷：568引用：4难度：0.5
解析
25．在平面直角坐标系中，点A（0，a）在y轴正半轴上，直线l平分坐标系的第二、四象限，点B是直线l上一动点．

（1）如图1，点A关于x轴的对称点为P点，则点P的坐标为
，当PB最短时，点B的坐标为
；（结果均用a表示）
（2）如图2，当AB⊥y轴，且垂足为点A时，以OA为边作正方形ABQO，M在x轴的正半轴，且OM＜OA，
以OM为边在x轴上方作正方形OMNH，连接AN，若QM=6，两个正方形面积之和为20，求△AHN的面积；
（3）如图3，当AB⊥y轴，且垂足为点A时，点F在线段OB上运动（不与端点重合），点C是线段BF的中点，连接AF，AC，以A为直角顶点，AF为直角边在第二象限内作等腰Rt△EAF，连接OE，交AC于点G探究线段OE与AC的关系，并说明理由．
组卷：191引用：1难度：0.2
解析