在平面直角坐标系中，点A（0，a）在y轴正半轴上，直线l平分坐标系的第二、四象限，点B是直线l上一动点．
（1）如图1，点A关于x轴的对称点为P点，则点P的坐标为 （0，-a）（0，-a），当PB最短时，点B的坐标为 （a2，-a2）（a2，-a2）；（结果均用a表示）
（2）如图2，当AB⊥y轴，且垂足为点A时，以OA为边作正方形ABQO，M在x轴的正半轴，且OM＜OA，
以OM为边在x轴上方作正方形OMNH，连接AN，若QM=6，两个正方形面积之和为20，求△AHN的面积；
（3）如图3，当AB⊥y轴，且垂足为点A时，点F在线段OB上运动（不与端点重合），点C是线段BF的中点，连接AF，AC，以A为直角顶点，AF为直角边在第二象限内作等腰Rt△EAF，连接OE，交AC于点G探究线段OE与AC的关系，并说明理由．
（
a
2
，-
a
2
）
（
a
2
，-
a
2
）
【考点】四边形综合题．
【答案】（0，-a）；
（
a
2
，-
a
2
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/22 16:0:8组卷：196引用：1难度：0.2
相似题
-
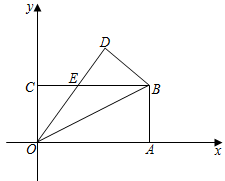1．如图，在平面直角坐标系中，长方形OABC的顶点A、C分别在x轴、y轴的正半轴上．点B的坐标为（8，4），将该长方形沿OB翻折，点A的对应点为点D，OD与BC交于点E．
（Ⅰ）证明：EO=EB；
（Ⅱ）点P是直线OB上的任意一点，且△OPC是等腰三角形，求满足条件的点P的坐标；
（Ⅲ）点M是OB上任意一点，点N是OA上任意一点，若存在这样的点M、N，使得AM+MN最小，请直接写出这个最小值．发布：2025/6/17 9:0:1组卷：305引用：2难度：0.3 -
2．请问读下列材料，并解答相应的问题
在Rt△ABC中、如果锐角A确定，那么角A的对边与邻边的比值随之确定，这个比叫做角A的正切，记作tanA，这是我们熟悉的三角函数中关于正切的定义．你不知道的是，世界上最早的正切函数表是由我国唐代一位叫做僧一行（683-727）的僧人在其所著《大衍历》中首次创作的．他通过某地影长的观测，求人阳天顶距进而求出该地各节气初日影长的方法，并为此编制了0度到80度的正切函数表．
我们摘取了部分正切函数表，如图所示，当角的度数是63.2度时，我们查表可知其对应的正切值为1.97，反之，如果已知一个角的正切值1.97，则这个角的度数是63.2度．
现已知矩形ABCD中，AD=4、AB=8，AC是对角线，点E是线段AB上的动点（点E不与A、B重合），点P是线段AC上的动点，（点P不与A、C重合）∠DPE=90°．角度 正切值 63.2 1.97 63.3 1.98 63.4 1.99 63.5 2.00 63.6 2.01 63.7 2.02
①若AE=AD，∠DPE=90°，测得∠DEP=63.5°，则查表可知tan∠DEP=，此时可求出线段PE=．（直接写出答案）
②若AE=3，∠DPE=90°，若此时点P恰好是AC中点，请直接写出tan∠DEP=．
③若AE的值不是3，那么在变化过程中，tan∠DEP是否发生变化？请说明理由．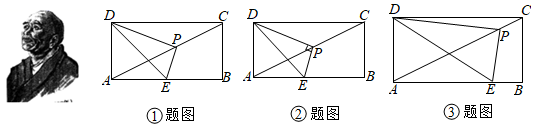
发布：2025/6/17 10:0:1组卷：58引用：1难度：0.4 -
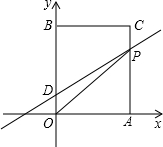3．如图在平面直角坐标系中，O是坐标原点，矩形OACB的顶点A，B分别在x轴、y轴上，已知OA=3，点D为y轴上一点，其坐标为（0，1），若连接CD，则CD=5，点P从点A出发以每秒1个单位的速度沿线段A-C-B的方向运动，当点P与点B重合时停止运动，运动时间为t秒
（1）求B，C两点坐标；
（2）求△OPD的面积S关于t的函数关系式；
（3）当点D关于OP的对称点E落在x轴上时，请直接写出点E的坐标，并求出此时的t值．发布：2025/6/17 10:30:2组卷：135引用：3难度：0.1
