2022-2023学年北京市十一学校晋元中学九年级（上）诊断数学试卷（12月份）

一、选择题（本题共24分，每小题3分）

• 1．下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的，其中是中心对称图形的是（　　）

  A．	B．
  C．	D．
  组卷：588引用：40难度：0.8

  解析

• 2．抛物线y=（x-2）²+1的顶点坐标是（　　）

  A．（-2，1）

  B．（2，1）

  C．（1，2）

  D．（1，-2）
  组卷：953引用：17难度：0.5

  解析

• 3．△ABC和△DEF是两个等边三角形，AB=2，DE=4，则△ABC与△DEF的面积比是（　　）

  A．1：2

  B．1：4

  C．1：8

  D．1：√2
  组卷：534引用：10难度：0.6

  解析

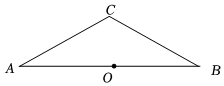• 4．在△ABC中，CA=CB，点O为AB中点．以点C为圆心，CO长为半径作⊙C，则⊙C与AB的位置关系是（　　）

  A．相交

  B．相切

  C．相离

  D．不确定
  组卷：1144引用：15难度：0.6

  解析

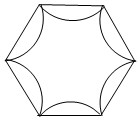• 5．小明将图案绕某点连续旋转若干次，每次旋转相同角度α，设计出一个外轮廓为正六边形的图案（如图），则α可以为（　　）

  A．30°

  B．60°

  C．90°

  D．120°
  组卷：1076引用：22难度：0.5

  解析

• 6．把长为2m的绳子分成两段，使较长一段的长的平方等于较短一段的长与原绳长的积．设较长一段的长为x m,依题意，可列方程为（　　）

  A．x2=2（2-x）

  B．x2=2（2+x）

  C．（2-x）2=2x

  D．x2=2-x
  组卷：639引用：12难度：0.8

  解析

• 7．如图，A，B，C是某社区的三栋楼，若在AC中点D处建一个5G基站，其覆盖半径为300m,则这三栋楼中在该5G基站覆盖范围内的是（　　）

  A．A，B，C都不在	B．只有B
  C．只有A，C	D．A，B，C
  组卷：828引用：18难度：0.6

  解析

• 8．做随机抛掷一枚纪念币的试验，得到的结果如下表所示：
  

  抛掷次数m	500	1000	1500	2000	2500	3000	4000	5000
  “正面向上”的次数n	265	512	793	1034	1306	1558	2083	2598
  “正面向上”的频率 n m	0.530	0.512	0.529	0.517	0.522	0.519	0.521	0.520

  下面有3个推断：
  ①当抛掷次数是1000时，“正面向上”的频率是0.512，所以“正面向上”的概率是0.512；
  ②随着试验次数的增加，“正面向上”的频率总在0.520附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.520；
  ③若再次做随机抛掷该纪念币的试验，则当抛掷次数为3000时，出现“正面向上”的次数不一定是1558次．
  其中所有合理推断的序号是（　　）

  A．②

  B．①③

  C．②③

  D．①②③
  组卷：918引用：11难度：0.7

  解析

三、解答题（共55分，第17-23题，每题5分，第24题6分，第25-26题7分）

• 25．在平面直角坐标系xOy中，点A（x₁，y₁），B（x₂，y₂）在抛物线y=-x²+（2a-2）x-a²+2a上，其中x₁＜x₂．
  （1）求抛物线的对称轴（用含a的式子表示）；
  （2）①当x=a时，求y的值；
  ②若y₁=y₂=0，求x₁的值（用含a的式子表示）；
  （3）若对于x₁+x₂＜-5，都有y₁＜y₂，求a的取值范围．
  组卷：979引用：4难度：0.4

  解析

• 26．如图，在△ABC中，∠BAC=90°，AB=AC=1，延长CB，并将射线CB绕点C逆时针旋转90°得到射线l,D为射线l上一动点，点E在线段CB的延长线上，且BE=CD，连接DE，过点A作AM⊥DE于M．
  （1）依题意补全图，用等式表示线段DM与ME之间的数量关系，并证明；
  （2）取BE的中点N，连接AN，添加一个条件：CD的长为

  ，使得AN=

  1

  2

  DE成立，并证明．
  
  组卷：874引用：7难度：0.4

  解析