当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省抚顺市六校协作体高一（下）期末数学试卷

发布：2024/6/23 8:0:10

一、单项选择题：本题共8小题，每小题5分，共40分，每题四个选项只有一个符合题目要求。

1．已知i为虚数单位若复数
z
=
4
-
i
2
2
-
i
，则
z
的虚部是（　　）
A．1 B．-1 C．i D．-i
组卷：37引用：2难度：0.8
解析
2．若扇形的面积为
π
2
，半径为4，则该扇形的圆心角为（　　）
A．
π
4
B．
π
6
C．
π
8
D．
π
16
组卷：180引用：3难度：0.8
解析
3．设
a
，
b
是非零向量，“
a
|
a
|
=
b
|
b
|
”是“
a
=
b
”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：300引用：8难度：0.7
解析
4．下列命题正确的是（　　）
（1）已知平面α和直线m,n,若m∥α，n⊂α，则m∥n；
（2）已知平面α，β和直线m,n,且m,n为异面直线，m⊥α，n⊥β．若直线l满足l⊥m,l⊥n,l⊄α，l⊄β，则α与β相交，且交线平行于l；
（3）已知平面α，β和直线m,n,若m⊂α，n⊂α，m∥β，n∥β，则α∥β；
（4）在三棱锥P-ABC中，PA⊥PB，PB⊥PC，PC⊥PA，垂足都为P，则P在底面上的射影是三角形ABC的垂心
A．（2）（4） B．（2）（3）（4） C．（3）（4） D．（1）（2）
组卷：41引用：2难度：0.5
解析
5．已知函数f（x）=cos⁴x-2sinxcosx-sin⁴x,则f（x）的最小正周期为（　　）
A．2π B．π C．
π
2
D．
π
4
组卷：230引用：4难度：0.7
解析
6．已知函数y=2-a^x-2（a＞0，且a≠1）的图象过定点P，O为坐标原点，射线OP是角θ的终边，则
sinθ
-
2
cosθ
2
sinθ
+
cosθ
的值为（　　）
A．
-
5
4
B．
3
4
C．
-
3
4
D．
-
3
2
组卷：288引用：4难度：0.7
解析
7．设
β
∈
（
0
，
π
2
）
，若sinα=3sin（α+2β），则tan（α+2β）的最小值为（　　）
A．
-
2
4
B．
2
4
C．
-
2
2
D．
2
2
组卷：307引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（17题10分，18题-22题每题12分，合计70分）

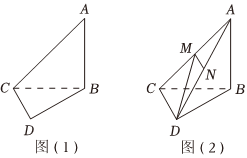21．如图（1），平面四边形ABDC中，∠ABC=∠D=90°，AB=BC=2，CD=1，将△ABC沿BC边折起如图（2），使 _____，点M，N分别为AC，AD中点．在题目横线上选择下述其中一个条件，然后解答此题．①
AD
=
7
．②AC为四面体ABDC外接球的直径．③平面ABC⊥平面BCD．
（1）判断直线MN与平面ABD是否垂直，并说明理由；
（2）求直线DM和BC所成的角的余弦值．
组卷：64引用：1难度：0.6
解析
22．已知函数f（x）=
3
sin（ωx+φ）-2cos²（
ωx
+
φ
2
）+1（ω＞0，0＜φ＜π）为奇函数，且f（x）图象的相邻两对称轴间的距离为
π
2
．
（1）当
x
∈
[
-
π
4
，
π
2
]
时，求f（x）的单调递减区间；
（2）将函数f（x）的图象向右平移
π
6
个单位长度，再把横坐标缩小为原来的
1
2
（纵坐标不变），得到函数y=g（x）的图象，记方程g（x）=
4
3
在
x
∈
[
π
6
，
4
π
3
]
上的根从小到大依次为x₁，x₂，x₃，…，x_n，试确定n的值，并求x₁+2x₂+2x₃+…+2x_n-1+x_n的值．
组卷：267引用：4难度：0.4
解析