2021-2022学年湖北省随州市曾都区八年级（上）期末数学试卷

一、选择题（本题共10小题，每小题3分，共30分．每小题给出的四个选项中只有一项是符合题目要求的）

• 1．要使分式

  1

  x

  -

  1

  有意义，则x的取值范围是（　　）

  A．x＞1

  B．x≠1

  C．x＜1

  D．x≠-1
  组卷：442引用：13难度：0.8

  解析

• 2．下列四种垃圾分类回收标识中，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：362引用：6难度：0.9

  解析

• 3．KN95型口罩可以保护在颗粒物浓度很高的空间中工作的人不被颗粒物侵害，也可以帮助人们预防传染病．“KN95”表示此类型的口罩能过滤空气中95%的粒径约为0.0000003m的非油性颗粒．其中，0.0000003用科学记数法表示为（　　）

  A．3×10-6

  B．3×10-7

  C．0.3×10-6

  D．0.3×10-7
  组卷：1178引用：28难度：0.8

  解析

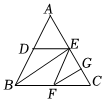• 4．如图，在△ABC中，D，E，F分别是边AB，AC，BC的中点，G为线段EC的中点，下列四条线段中，是△ABC的中线的是（　　）

  A．线段DE

  B．线段BE

  C．线段EF

  D．线段FG
  组卷：333引用：2难度：0.8

  解析

• 5．下列计算正确的是（　　）

  A．3x2•2x=6x3	B．x6÷x3=x2
  C．（3a）2=3a2	D．（a+b）2=a2+b2
  组卷：296引用：50难度：0.9

  解析

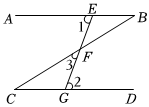• 6．如图，∠1=∠2=65°，∠C=30°，则下列结论错误的是（　　）

  A．AB∥CD

  B．∠B=30°

  C．∠EFC=95°

  D．∠3=35°
  组卷：470引用：2难度：0.7

  解析

• 7．到三角形三边的距离相等的点是（　　）

  A．三角形三边的中垂线的交点

  B．三角形三条高所在直线的交点

  C．三角形三条中线的交点

  D．三角形三条角平分线的交点
  组卷：83引用：1难度：0.7

  解析

• 8．数学家斐波那契编写的《算经》中有如下问题：一组人平分10元钱，每人分得若干；若再加上6人，平分40元钱，则第二次每人所得与第一次相同，求第一次分钱的人数，设第一次分钱的人数为x人，则可列方程（　　）

  A． 10 x = 40 x - 6	B． 40 x = 10 x - 6
  C． 10 x = 40 x + 6	D．10x=40（x+6）
  组卷：600引用：15难度：0.8

  解析

三、解答题（本题共8小题，共72分．解答应写出必要的演算步骤、文字说明或证明过程）

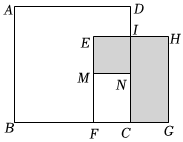• 23．在求代数式值的问题中，有时通过观察式子的特点，可以找到较为简单的解法．
  例如，若x满足（x-2）（x-5）=10，求（x-2）²-（x-5）²的值，可以按下列的方法来解：
  解：设（x-2）=a,（x-5）=b,则ab=（x-2）（x-5）=10，a-b=（x-2）-（x-5）=3，
  ∴（a+b）²=（a-b）²+4ab=49，∴a+b=±7，
  ∴（x-2）²-（x-5）²=a²-b²=（a+b）（a-b）=±7×3=±21．
  请仿照上面的方法求解下面的问题：
  （1）若x满足（x-4）（x-9）=6，求（x-4）²+（x-9）²的值；
  （2）将正方形ABCD和正方形EFGH按如图所示摆放，点F在BC边上，EH与CD交于点I，且ID=1，CG=2，长方形EFCI的面积为24，以CF为边作正方形CFMN．设AD=x,
  ①用含x的代数式直接表示EF和CF的长；
  ②求图中阴影部分的面积．
  组卷：220引用：2难度：0.7

  解析

• 24．在平面直角坐标系中，点A的坐标为（6，0），点B在第一象限，△OAB为等边三角形，点C为y轴上一动点，以AC为边在AC下方作等边△PAC，连接BC，OP．
  （1）如图1，当点C在y轴正半轴上时，求证：OP=BC；
  （2）如图2，当点C在y轴负半轴上时，请在图2中补全图形，并判断（1）中的结论是否还成立？并说明理由；
  （3）设点P的横坐标为m,根据上述探究，请问OP的长是否有最小值？若有，直接写出OP长的最小值及此时m的值；若没有，请简要说明理由．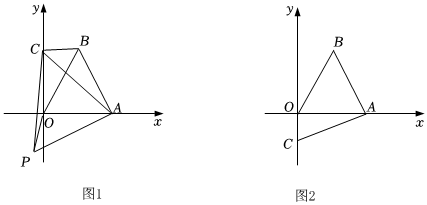
  
  组卷：140引用：1难度：0.5

  解析