当前位置：试卷中心 > 试卷详情

2022-2023学年河南省部分学校高三（上）押题数学试卷（理科）（一）

发布：2024/9/27 15:0:1

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合
A
=
{
x
|
4
-
x
x
-
1
≥
0
}
，B={y|y=log₄x,x∈A}，则A∪B=（　　）
A．（0，4] B．[1，2] C．[1，4] D．[2，4]
组卷：7引用：2难度：0.7
解析
2．抛掷一枚骰子两次，第一次得到的点数记为x,第二次得到的点数记为y,则平面直角坐标系xOy中，点（x,y）到原点O的距离不大于4的概率为（　　）
A．
1
6
B．
7
36
C．
2
9
D．
1
4
组卷：9引用：6难度：0.7
解析
3．已知tan（α+β），tan（α-β）是方程x²+5x+6=0的两个根，则tan2α=（　　）
A．-1 B．1 C．-2 D．2
组卷：70引用：6难度：0.7
解析
4．已知z₁，z₂∈C，且|z₁|=1，若z₁+z₂=i,则|z₂|的最大值是（　　）
A．5 B．4 C．3 D．2
组卷：4引用：2难度：0.6
解析
5．执行如图的程序框图，输出的n=（　　）
A．3 B．4 C．5 D．6
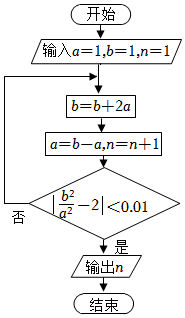组卷：687引用：14难度：0.7
解析
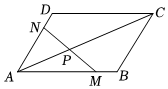6．如图，在平行四边形ABCD中，M，N分别为AB，AD上的点，且
AM
=
4
5
AB
，
AN
=
2
3
AD
，连接AC，MN交于P点，若
AP
=
λ
AC
，则λ的值为（　　）
A．
3
5
B．
5
7
C．
4
11
D．
8
15
组卷：376引用：5难度：0.7
解析
7．日常生活中，我们定义一个食堂的菜品受欢迎程度为菜品新鲜度．其表达式为
R
=
σ
N
，其中R的取值与在本窗口就餐人数有关，其函数关系式我们可简化为
y
=
470
1
+
8
.
6
-
5
.
75
x
，其中y为就餐人数（本窗口），x为餐品新鲜度（R），则当N=2，σ=2000时，y近似等于（　　）（已知8.6^-5.75≈4.23×10^-6）
A．470 B．471 C．423 D．432
组卷：34引用：3难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。

22．已知在平面直角坐标系xOy中，直线l的参数方程为
x
=
2
+
t
,
y
=
2
3
+
3
t
（t为参数），以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为
ρ
=
1
ρ
+
2
3
cosθ
．
（1）求直线l的极坐标方程以及曲线C的参数方程；
（2）若直线l与曲线C交于M，N两点，求
1
|
OM
|
2
+
1
|
ON
|
2
的值．
组卷：140引用：6难度：0.5
解析
23．若a＞0，b＞0，4a+b=ab.
（Ⅰ）求a+b的最小值；
（Ⅱ）当a+b取得最小值时，a,b的值满足不等式|x-a|+|x-b|≥t²-2t对任意的x∈R恒成立，求t的取值范围．
组卷：644引用：6难度：0.3
解析