2022-2023学年湖南省五市十校教研教改共同体高一（下）期中数学试卷

一、单选题

• 1．复数z=1+i的虚部是（　　）

  A．1

  B．-1

  C．i

  D．-i
  组卷：20引用：7难度：0.9

  解析

• 2．若正实数a、b满足a+2b=1，则当ab取最大值时，a的值是（　　）

  A． 1 2

  B． 1 4

  C． 1 6

  D． 1 8
  组卷：683引用：5难度：0.7

  解析

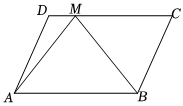• 3．如图，在平行四边形ABCD中，

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  CM

  =

  4

  MD

  ，则

  AM

  =（　　）

  A． a + 1 5 b

  B． 1 5 a + b

  C． 1 5 a - b

  D． a - 1 5 b
  组卷：59引用：3难度：0.7

  解析

• 4．已知

  a

  =

  cos

  π

  3

  ，b=2^0.2，

  c

  =

  lo

  g

  2

  3

  ，则（　　）

  A．b＞c＞a

  B．b＞a＞c

  C．a＞c＞b

  D．a＞b＞c
  组卷：176引用：4难度：0.7

  解析

• 5．下列关于平面图形的直观图的叙述中，正确的是（　　）

  A．等腰三角形的直观图仍是一个等腰三角形

  B．若某一平面图形的直观图面积为a,则原图形面积为 2 2 a

  C．原图形中相等的线段，其直观图也一定相等

  D．若三角形的周长为12，则其直观图的周长为6
  组卷：34引用：3难度：0.7

  解析

• 6．函数f（x）=log₂x-sinx+

  1

  2

  的零点所在的区间为（　　）

  A．（ 1 4 ， 1 2 ）

  B．（ 1 2 ，1）

  C．（1，2）

  D．（2，3）
  组卷：89引用：2难度：0.6

  解析

• 7．若△ABC为锐角三角形，则（　　）

  A．sinA＞sinB	B．cosA＞cosB
  C．sin（cosA）＞sin（sinB）	D．cos（cosA）＞cos（sinB）
  组卷：78引用：3难度：0.6

  解析

四、解答题

• 21．对于函数f（x），g（x），若存在实数k使得函数h（x）=kf（x）•g（x），那么称函数h（x）为f（x），g（x）的k积函数．
  （1）设函数f（x）=sinx,

  g

  （

  x

  ）

  =

  cos

  （

  x

  +

  2

  π

  3

  ）

  ，

  h

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  3

  ）

  +

  3

  ，试判断h（x）是否为f（x），g（x）的k积函数？若是，请求出k的值；若不是，请说明理由；
  （2）设函数

  f

  （

  x

  ）

  =

  mx

  +

  n

  x

  （其中m＞0，n＞0，x＞0），且函数f（x）图象的最低点坐标为（2，4），若函数g（x）=f（2-x），h（x）是f（x），g（x）的1积函数，且对于任意实数x∈（0，2），h（x）≥a恒成立，求实数a的取值范围．
  组卷：32引用：3难度：0.5

  解析

• 22．在锐角△ABC中，角A，B，C所对的边分别是a,b,c,已知b=2，

  a

  b

  =

  3

  3

  sinC+cosC．
  （1）求角B；
  （2）若M是△ABC内的一动点，且满足

  BM

  =

  MA

  +

  MC

  ，则|

  BM

  |是否存在最大值？若存在，请求出最大值及取最大值的条件；若不存在，请说明理由；
  （3）若D是△ABC中AC上的一点，且满足

  BA

  •

  BD

  |

  BA

  |

  =

  BD

  •

  BC

  |

  BC

  |

  ，求AD：DC的取值范围．
  组卷：344引用：6难度：0.3

  解析