2023年重庆市南开中学高考数学第四次质检试卷

一、单项选择题：本题共8小题．每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求．

• 1．已知复数z满足z（1+i）=2i,其中i为虚数单位，则复数z的模|z|=（　　）

  A．1

  B． 2

  C．2

  D． 2 2
  组卷：163引用：8难度：0.8

  解析

• 2．已知集合A={-1，0}，B={1，2}，则集合C={z|z=x²+y²，x∈A，y∈B}的真子集个数为（　　）

  A．7

  B．8

  C．15

  D．16
  组卷：213引用：3难度：0.8

  解析

• 3．已知直线l₁：（m-2）x-3y-1=0与直线l₂：mx+（m+2）y+1=0相互平行，则实数m的值是（　　）

  A．-4

  B．1

  C．-1

  D．6
  组卷：521引用：13难度：0.7

  解析

• 4．公元五世纪，数学家祖冲之估计圆周率π的范围是：3.1415926＜π＜3.1415927，为纪念祖冲之在圆周率方面的成就，把3.1415926称为“祖率”，这是中国数学的伟大成就．小明是个数学迷，他在设置手机的数字密码时，打算将圆周率的前6位数字3，1，4，1，5，9进行某种排列得到密码．如果排列时要求两个1不相邻，那么小明可以设置的不同密码有（　　）个

  A．240

  B．360

  C．600

  D．720
  组卷：310引用：11难度：0.8

  解析

• 5．已知函数

  f

  （

  x

  ）

  =

  ln

  （

  x

  2

  +

  1

  -

  x

  ）

  +

  1

  ，正实数a,b满足f（2a）+f（b-4）=2，则

  4

  b

  a

  +

  a

  2

  ab

  +

  b

  2

  的最小值为（　　）

  A．1

  B．2

  C．4

  D． 65 8
  组卷：372引用：4难度：0.6

  解析

• 6．已知函数f（x）=

  x + 1 ， x ≤ 0

  | x - 1 x | ， x ＞ 0

  ，若关于x的方程f²（x）+（m-4）f（x）+2（2-m）=0有五个不同的实数根，则实数m的取值范围是（　　）

  A．[1，3）

  B．（0，2）

  C．[1，2）

  D．（0，1）
  组卷：481引用：5难度：0.5

  解析

• 7．已知点P为抛物线y²=2px（p＞0）上一动点，点Q为圆C：（x+1）²+（y-4）²=1上一动点，点F为抛物线的焦点，点P到y轴的距离为d,若|PQ|+d的最小值为2，则p=（　　）

  A． p = 1 2

  B．p=1

  C．p=2

  D．p=4
  组卷：231引用：6难度：0.6

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知函数f（x）=e^x（x-2a）+ax+2，a∈R．
  （1）当a=1时，求曲线f（x）在点（1，f（1））处的切线方程；
  （2）若不等式f（x）≥0对∀x≥0恒成立，求实数a的范围；
  （3）证明：当

  n

  ∈

  N

  *

  ，

  1

  +

  1

  2

  +

  1

  3

  +

  ⋯

  +

  1

  n

  ＜

  ln

  （

  2

  n

  +

  1

  ）

  ．
  组卷：141引用：3难度：0.4

  解析

• 22．已知椭圆

  C

  1

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

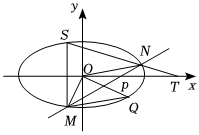  的左右焦点分别为F₁，F₂，右顶点为A，上顶点为B，O为坐标原点，|OA|=2|OB|．
  （1）若△BF₁F₂的面积为

  4

  3

  ，求椭圆C₁的标准方程；
  （2）如图，过点P（1，0）作斜率k（k＞0）的直线l交椭圆C₁于不同两点M，N，点M关于x轴对称的点为S，直线SN交x轴于点T，点P在椭圆的内部，在椭圆上存在点Q，使

  OM

  +

  ON

  =

  OQ

  ，记四边形OMQN的面积为S₁，求

  OT

  •

  OQ

  -

  S

  2

  1

  k

  的最大值．
  组卷：161引用：4难度：0.3

  解析