2022-2023学年湖北省黄冈市、黄石市、鄂州市三市联考高一（下）期末数学试卷

一、选择题（每小题5分，共8小题40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知复数

  z

  =

  2

  +

  i

  2023

  1

  -

  i

  ，则

  z

  =

  2

  +

  i

  2023

  1

  -

  i

  的虚部为（　　）

  A． 1 2

  B． 1 2 i

  C． 3 2

  D． 3 2 i
  组卷：26引用：2难度：0.8

  解析

• 2．已知A（2，3），B（5，1），C（m,2），且A，B，C三点共线，则m=（　　）

  A． 1 2

  B． 3 2

  C． 5 2

  D． 7 2
  组卷：112引用：3难度：0.7

  解析

• 3．某工厂生产A，B，C三种不同型号的产品，产品数量之比为4：3：k,现用分层随机抽样方法抽取一个容量为140的样本．已知C型产品抽取了56件，则A型产品抽取的件数为（　　）

  A．36

  B．48

  C．56

  D．60
  组卷：43引用：2难度：0.8

  解析

• 4．下列说法正确的是（　　）

  A．两两相交的三条直线确定一个平面

  B．如果直线a,b和平面α满足a∥α，b∥α，那么a∥b

  C．过平面外一点有且只有一条直线与这个平面垂直

  D．若平面α⊥平面β，平面β⊥平面γ，那么平面α⊥平面γ
  组卷：40引用：2难度：0.5

  解析

• 5．已知△ABC中，AB=6，BC=8，∠B=60°，则AB边上的中线长为（　　）

  A． 78

  B．8

  C．7

  D．6
  组卷：140引用：1难度：0.6

  解析

• 6．已知空间中∠POA=∠POB=60°，∠AOB=90°，∠AOB=90°，直线OP与平面AOB所成的角为θ，则cosθ为（　　）

  A． 2 2

  B． 3 3

  C． 1 2

  D． 1 3
  组卷：129引用：1难度：0.6

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  8

  cos

  （

  x

  -

  θ

  +

  π

  3

  ）

  cos

  （

  x

  -

  θ

  -

  π

  3

  ）

  +

  2

  （

  0

  ＜

  θ

  ＜

  π

  2

  ）

  的一条对称轴为

  x

  =

  π

  6

  ，且在区间[0，t]上值域为[2，4]，则实数t的最大值为（　　）

  A． 5 π 6

  B． 2 π 3

  C． 5 π 12

  D． π 3
  组卷：69引用：3难度：0.5

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．如图，在△ABC中，AB=10，AC=3，cos∠ACB=-

  5

  27

  ，点D，E分别在边BC，AB上，且BD=2DC，CE⊥AC，AD与CE交于点M．
  （1）设

  CB

  =

  a

  ，

  CA

  =

  b

  ，试用

  a

  ，

  b

  表示

  CE

  ；
  （2）求AM的长．
  组卷：44引用：1难度：0.6

  解析

• 22．如图①，在矩形ABCD中，

  AB

  =

  2

  AD

  =

  4

  2

  ，

  E

  ，E为CD的中点，如图②，将
  △AED沿AE折起，点M在线段CD上．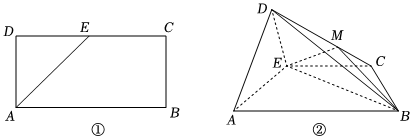
  
  （1）若DM=2MC，求证AD∥平面MEB；
  （2）若平面AED⊥平面BCEA，是否存在点M，使得平面DEB与平面MEB垂直？若存在，求此时三棱锥B-DEM的体积，若不存在，说明理由．
  组卷：100引用：4难度：0.5

  解析