2023年山西省阳泉一中高考数学适应性试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．若全集U={1，2，3，4，5，6}，集合A={1，3，6}，B={2，3，4}，则A∩∁_UB=（　　）

  A．{3}

  B．{1，6}

  C．{5，6}

  D．{1，3}
  组卷：4104引用：21难度：0.9

  解析

• 2．若复数z满足（4+2i）z=（3-i）²，则|z|=（　　）

  A．1

  B． 2

  C． 3

  D． 5
  组卷：59引用：4难度：0.9

  解析

• 3．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  1

  ，

  1

  ）

  ，

  c

  =

  （

  m

  ,

  2

  ）

  ，且

  （

  a

  -

  2

  b

  ）

  ⊥

  c

  ，则实数m=（　　）

  A．-1

  B．0

  C．1

  D．任意实数
  组卷：387引用：11难度：0.7

  解析

• 4．在《九章算术•商功》中将正四面形棱台体（棱台的上、下底面均为正方形）称为方亭．在方亭ABCD-A₁B₁C₁D₁中，AB=2A₁B₁=4，四个侧面均为全等的等腰梯形且面积之和为

  12

  2

  ，则该方亭的体积为（　　）

  A． 14 3

  B． 28 3

  C． 14 2 3

  D． 28 2 3
  组卷：92引用：3难度：0.6

  解析

• 5．中国空间站的主体结构包括天和核心实验舱、问天实验舱和梦天实验舱，假设空间站要安排甲、乙等5名航天员开展实验，三舱中每个舱至少一人至多二人，则甲乙不在同一实验舱的种数有（　　）

  A．60

  B．66

  C．72

  D．80
  组卷：214引用：7难度：0.7

  解析

• 6．圆锥的母线长为4，侧面积是底面积的

  4

  3

  倍，过圆锥的两条母线作圆锥的截面，则该截面面积的最大值是（　　）

  A．8

  B． 4 7

  C．3 7

  D． 3 6
  组卷：89引用：2难度：0.7

  解析

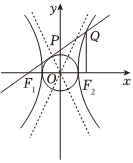• 7．如图，已知F₁，F₂分别为双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦点，O为坐标原点，其渐近线与圆x²+y²=a²在第二象限交于点P，若直线PF₁交双曲线右支于点Q，且|PQ|＞|QF₂|+

  2

  5

  |OF₂|，则双曲线的心率可能是（　　）

  A． 5 4

  B． 7 5

  C． 3 2

  D． 5 3
  组卷：73引用：1难度：0.4

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

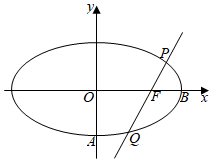• 21．已知椭圆方程

  x

  2

  2

  +

  y

  2

  =

  1

  右焦点F、斜率为k的直线l交椭圆于P、Q两点．
  （1）求椭圆的两个焦点和短轴的两个端点构成的四边形的面积；
  （2）当直线l的斜率为1时，求△POQ的面积；
  （3）在线段OF上是否存在点M（m,0），使得以MP、MQ为邻边的平行四边形是菱形？若存在，求出m的取值范围；若不存在，说明理由．
  组卷：522引用：10难度：0.5

  解析

• 22．已知函数f（x）=x²-axlnx+1+a,a∈R，f′（x）为f（x）的导函数．
  （1）讨论f′（x）的极值；
  （2）若存在t∈[2，e]，使得不等式f（t）＜0成立，求a的取值范围．
  组卷：138引用：4难度：0.3

  解析