当前位置：试卷中心 > 试卷详情

2023-2024学年浙江省衢州市江山中学高二（上）段考数学试卷（10月份）

发布：2024/9/5 6:0:10

一、单选题（本大题共8小题，每小题5分，共40分.）

1．已知集合A={-1，0，1，2，3}，B={x|-1＜x＜2}，则A∩B=（　　）
A．{-1，0} B．{-1，0，1} C．{0，1} D．{0，1，2}
组卷：121引用：16难度：0.8
解析
2．在复平面内，复数（1+2i）i对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：301引用：13难度：0.8
解析
3．以点A（-5，4）为圆心，4为半径的圆的方程是（　　）
A．（x+5）²+（y-4）²=25 B．（x-5）²+（y+4）²=16
C．（x+5）²+（y-4）²=16 D．（x-5）²+（y+4）²=25
组卷：135引用：2难度：0.9
解析
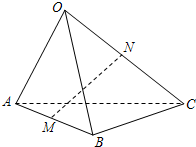4．已知三棱锥O-ABC，点M，N分别为AB，OC的中点，且
OA
=
a
，
OB
=
b
，
OC
=
c
，用
a
，
b
，
c
表示
MN
，则
MN
等于（　　）
A．
1
2
（
b
+
c
-
a
）
B．
1
2
（
a
+
b
-
c
）
C．
1
2
（
a
-
b
+
c
）
D．
1
2
（
c
-
a
-
b
）
组卷：2893引用：41难度：0.9
解析
5．已知a=log_0.23，b=2^0.3，c=0.3^0.2，则a、b、c的大小关系为（　　）
A．a＜b＜c B．b＜c＜a C．a＜c＜b D．b＜a＜c
组卷：232引用：7难度：0.8
解析
6．游戏《王者荣耀》对青少年的不良影响巨大，被戏称为“王者农药”．某班40名学生都有着不低的游戏段位等级，其中白银段位22人，其余人都是黄金或铂金段位，从该班40名学生中随机抽取一名学生，若抽得黄金段位的概率是0.25，则抽得铂金段位的概率是（　　）
A．0.20 B．0.22 C．0.25 D．0.42
组卷：74引用：2难度：0.9
解析
7．《几何原本》是古希腊数学家欧几里得的一部不朽之作，其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥，若某直角圆锥内接于一球（圆锥的顶点和底面上各点均在该球面上），且该圆锥的侧面积为
2
π
，则此球的表面积为（　　）
A．
2
π
B．2π C．
2
2
π
D．4π
组卷：73引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，第17题10分，其余每小题10分，共70分.解答应写出必要的文字说明、证明过程或演算步骤.）

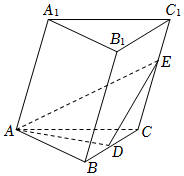21．如图，在三棱柱ABC-A₁B₁C₁中，AB=AC=2，D为BC的中点，平面BB₁C₁C⊥平面ABC．
（1）证明：AD⊥BB₁；
（2）已知四边形BB₁C₁C是边长为2的菱形，且∠B₁BC=60°，问在线段CC₁上是否存在点E，使得平面EAD与平面EAC的夹角的余弦值为
15
5
，若存在，求出CE的长度，若不存在，请说明理由．
组卷：181引用：3难度：0.5
解析
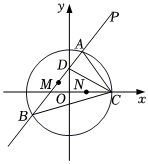22．如图，在平面直角坐标系xOy中，已知点P（2，4），圆O：x²+y²=4与x轴的正半轴的交点是Q，过点P的直线l与圆O交于不同的两点A，B．
（1）若直线l与y轴交于D，且
DP
•
DQ
=16，求直线l的方程；
（2）设直线QA，QB的斜率分别是k₁，k₂，求k₁+k₂的值；
（3）设AB的中点为M，点N（
4
3
，0），若MN=
13
3
OM，求△QAB的面积．
组卷：522引用：5难度：0.3
解析