2023年西藏林芝第二高级中学高考数学四模试卷（文科）

一、选择题（本大题共12小题，每小题5分，共60分）．

• 1．已知集合A={x|x²-3x-4＜0}，B={-4，1，3，5}，则A∩B=（　　）

  A．{-4，1}

  B．{1，5}

  C．{3，5}

  D．{1，3}
  组卷：4659引用：31难度：0.9

  解析

• 2．已知i为虚数单位，则

  4

  -

  3

  i

  1

  +

  i

  =（　　）

  A． 1 2 + 7 2 i

  B． 1 2 - 7 2 i

  C． 5 2 + 3 2 i

  D． 5 2 - 3 2 i
  组卷：35引用：4难度：0.8

  解析

• 3．某校高一学生550人，高二学生500人，高三学生450人，现有分层抽样，在高三抽取了18人，则高二应抽取的人数为（　　）

  A．24

  B．22

  C．20

  D．18
  组卷：276引用：6难度：0.8

  解析

• 4．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．
  
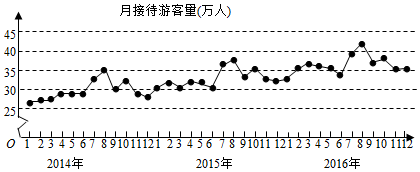
  根据该折线图，下列结论错误的是（　　）

  A．月接待游客逐月增加

  B．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

  C．各年的月接待游客量高峰期大致在7，8月

  D．年接待游客量逐年增加
  组卷：160引用：3难度：0.9

  解析

• 5．已知函数f（x）的导函数g（x）=（x-1）（x²-3x+a），若1不是函数f（x）的极值点，则实数a的值为（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：107引用：6难度：0.5

  解析

• 6．在△ABC中，cosC=

  2

  3

  ，AC=4，BC=3，则tanB=（　　）

  A． 5

  B．2 5

  C．4 5

  D．8 5
  组卷：5572引用：17难度：0.6

  解析

• 7．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  m

  ,

  2

  -

  m

  ）

  ，若

  a

  ⊥

  b

  ，则

  |

  b

  |

  =（　　）

  A． 3

  B． 5

  C．2 3

  D．2 5
  组卷：386引用：14难度：0.9

  解析

三、解答题：（本大题共5小题，共70分）．

• 21．设函数f（x）=a²x²+ax-3lnx+1，其中a＞0．
  （1）讨论f（x）的单调性；
  （2）若y=f（x）的图像与x轴没有公共点，求a的取值范围．
  组卷：6793引用：11难度：0.6

  解析

[选修4—4：坐标系与参数方程]

• 22．在直角坐标系xOy中，曲线C₁的参数方程为

  x = 2 + t 6 ，

  y = t

  （t为参数），曲线C₂的参数方程为

  x = - 2 + s 6 ，

  y = - s

  （s为参数）．
  （1）写出C₁的普通方程；
  （2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C₃的极坐标方程为2cosθ-sinθ=0，求C₃与C₁交点的直角坐标，及C₃与C₂交点的直角坐标．
  组卷：1545引用：9难度：0.7

  解析