当前位置：试卷中心 > 试卷详情

2022-2023学年江西省九江市彭泽第二高级中学高一（下）期末数学试卷

发布：2024/6/16 8:0:10

一、单选题（每题5分，共40分）

1．设A={x|-1≤x＜2}，B={x|x＜a}，若A∩B≠∅，则a的取值范围是（　　）
A．a＜2 B．a＞-2 C．a＞-1 D．-1＜a≤2
组卷：2228引用：45难度：0.7
解析
2．下列各角中与
π
6
终边相同的角是（　　）
A．
-
π
6
B．
17
π
6
C．
π
6
+
kπ
，
k
∈
Z
D．
π
6
+
2
kπ
，
k
∈
Z
组卷：126引用：1难度：0.7
解析
3．若C是线段AB的中点，则
AC
+
BC
=（　　）
A．
AB
B．
BA
C．
0
D．以上均不正确
组卷：222引用：3难度：0.9
解析
4．在△ABC中，“AB²+BC²＜AC²”是“△ABC为钝角三角形”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：78引用：6难度：0.8
解析
5．已知
α
∈
（
0
，
π
2
）
，
cos
2
α
+
sin
2
α
=
1
5
，则tanα=（　　）
A．-2 B．2 C．
1
2
D．
1
3
组卷：77引用：1难度：0.7
解析
6．已知向量
OA
=（cosβ，sinβ），将向量
OA
绕坐标原点O逆时针旋转θ角得到向量
OB
（0＜θ＜90°），则下列说法不正确的是（　　）
A．|
OA
|+|
OB
|＞|
OA
-
OB
| B．|
AB
|＜
2
C．|
OA
+
OB
|=|
OA
-
OB
| D．（
OA
+
OB
）⊥（
OA
-
OB
）
组卷：493引用：3难度：0.9
解析
7．《九章算术》中“开立圆术”曰：“置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径”．“开立圆术”相当于给出了已知球的体积V，求其直径d,公式为
d
=
3
16
9
V
．如果球的半径为
1
3
，根据“开立圆术”的方法求球的体积为（　　）
A．
4
π
81
B．
π
6
C．
4
81
D．
1
6
组卷：186引用：9难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（共70分）

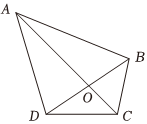21．如图，A，B两点都在河的对岸（不可到达），为了测量A，B两点间的距离，在A，B两点的对岸选定两点C，D，测得CD=a,并且在C，D两点分别测得∠ACB=60°，∠ACD=45°，∠BDC=30°，∠BDA=75°，
（1）求A，B两点间的距离；
（2）设AC与BD相交于点O，记△AOD与△BOC的面积分别为S₁，S₂，求S₁-S₂．
组卷：132引用：3难度：0.5
解析
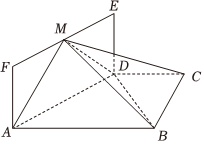22．如图，平面ADEF⊥平面ABCD，四边形ADEF为矩形，且M为线段EF上的动点，AB∥CD，∠ABC=90°，AD=2DE，AB=2CD=2BC=2．
（1）当M为线段EF的中点时，
（ⅰ）求证：AM⊥平面BDM；
（ⅱ）求直线AM与平面MBC所成角的正弦值；
（2）记直线AM与平面MBC所成角为α，平面MAD与平面MBC的夹角为β，是否存在点M使得α=β？若存在，求出FM；若不存在，说明理由．
组卷：200引用：6难度：0.5
解析