2022-2023学年河北省石家庄二中高三（下）月考数学试卷（4月份）

一、单选题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

• 1．已知集合A={x|x²＜2x}，集合B={x|log₂（x-1）＜1}，则A∩B=（　　）

  A．{x|0＜x＜3}

  B．{x|1＜x＜2}

  C．{x|2≤x＜3}

  D．{x|0＜x＜2}
  组卷：116引用：5难度：0.8

  解析

• 2．已知复数z满足

  1

  +

  3

  i

  z

  =

  3

  +

  4

  i

  ，则

  |

  z

  |

  =（　　）

  A． 2 5 5

  B． 10 5

  C． 2 5

  D． 2 5
  组卷：76引用：5难度：0.8

  解析

• 3．积极参加公益活动是践行社会主义核心价值观的具体行动．现将包含甲、乙两人的5位同学分成2个小组分别去敬老院和老年活动中心参加公益活动，每个小组至少一人，则甲、乙两名同学不分在同一小组的安排方法的总数为（　　）

  A．12

  B．14

  C．15

  D．16
  组卷：193引用：6难度：0.6

  解析

• 4．剪纸是中国古老的传统民间艺术之一，剪纸时常会沿着纸的某条对称轴对折．将一张纸片先左右折叠，再上下折叠，然后沿半圆弧虚线裁剪，展开得到最后的图形，若正方形ABCD的边长为2，点P在四段圆弧上运动，则

  AP

  •

  AB

  的取值范围为（　　）
  

  A．[-1，3]

  B．[-2，6]

  C．[-3，9]

  D．[-3，6]
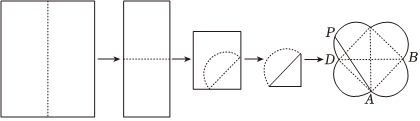  组卷：96引用：6难度：0.7

  解析

• 5．在正三棱柱ABC-A₁B₁C₁中，AB=2，AA₁=3，以C₁为球心，

  39

  3

  为半径的球面与侧面ABB₁A₁的交线长为（　　）

  A． 2 3 π 9

  B． 2 3 π 3

  C． 4 3 π 9

  D． 8 3 π 9
  组卷：141引用：5难度：0.6

  解析

• 6．利用“lnx≤x-1”可得到许多与n（n≥2且n∈N^*）有关的结论①

  ln

  （

  n

  +

  1

  ）

  ＜

  1

  +

  1

  2

  +

  1

  3

  +

  ⋯

  +

  1

  n

  ，②

  lnn

  ＞

  1

  2

  +

  1

  3

  +

  ⋯

  +

  1

  n

  ，③

  （

  1

  +

  1

  2

  ）

  （

  1

  +

  1

  2

  2

  ）

  ⋯

  （

  1

  +

  1

  2

  n

  ）

  ＞

  e

  ，④

  （

  1

  n

  ）

  n

  +

  （

  2

  n

  ）

  n

  +

  ⋯

  +

  （

  n

  n

  ）

  n

  ＜

  e

  e

  -

  1

  ，则结论正确的有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：55引用：3难度：0.3

  解析

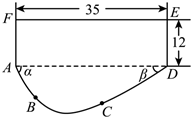• 7．某中学开展劳动实习，学生加工制作零件，零件的截面如图（单位：cm）所示，四边形AFED为矩形，AB，CD，FE均与圆O相切，B、C为切点，零件的截面BC段为圆O的一段弧，已知tanα=

  4

  3

  ，

  tanβ

  =

  3

  4

  ，则该零件的截面的周长为（　　）cm（结果保留π）．

  A．84+6π

  B．80+5π

  C．75+5π

  D．82+6π
  组卷：55引用：3难度：0.6

  解析

四、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.）

• 21．品酒师需定期接受酒味鉴别功能测试，通常采用的测试方法如下：拿出n（n∈N^*且n≥4）瓶外观相同但品质不同的酒让品酒师品尝，要求其按品质优劣为它们排序；经过一段时间，等其记忆淡忘之后，再让其品尝这n瓶酒，并重新按品质优劣为它们排序．这称为一轮测试，根据一轮测试中的两次排序的偏离程度的高低为其评分．现分别以a₁，a₂，a₃，…，a_n表示第一次排序时被排在1，2，3，…，n的n种酒在第二次排序时的序号，并令X=|1-a₁|+|2-a₂|+|3-a₃|+…+|n-a_n|，则X是对两次排序的偏离程度的一种描述．
  （1）证明：无论n取何值，X的可能取值都为非负偶数；
  （2）取n=4，假设在品酒师仅凭随机猜测来排序的条件下，a₁，a₂，a₃，a₄等可能地为1，2，3，4的各种排列，且各轮测试相互独立．
  ①求X的分布列和数学期望；
  ②若某品酒师在相继进行的三轮测试中，都有X≤2，则认为该品酒师有较好的酒味鉴别功能．求出现这种现象的概率，并据此解释该测试方法的合理性．
  组卷：257引用：3难度：0.5

  解析

• 22．已知f（x）=（e^x-1）sinx,x∈（0，2π）．
  （1）求f（x）在点P（π，f（π））的切线方程；
  （2）设g（x）=f（x）-x²，x∈（0，2π），判断g（x）的零点个数，并说明理由．
  组卷：142引用：5难度：0.2

  解析