当前位置：试卷中心 > 试卷详情

2022-2023学年福建省厦门大学附属科技中学八年级（下）期末数学试卷

发布：2024/7/14 8:0:9

一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）

1．下列二次根式是最简二次根式的是（　　）
A．
1
2
B．
7
C．
8
D．
4
组卷：127引用：5难度：0.8
解析
2．四边形ABCD是平行四边形，下列关系正确的是（　　）
A．AC=BD B．AC⊥BD C．AB=BC D．AB=CD
组卷：77引用：2难度：0.5
解析
3．正比例函数y=-
1
2
x的图象经过的象限是（　　）
A．第一、三象限 B．第二、四象限
C．第三、四象限 D．第一、二象限
组卷：659引用：7难度：0.8
解析
4．某学校要招聘一名教师，分笔试和面试两次考试，笔试、面试和最后得分的满分均为100分，竞聘教师的最后得分按笔试成绩：面试成绩=3：2的比例计算．在这次招聘考试中，某竞聘教师的笔试成绩为90分，面试成绩为80分，则该竞聘教师的最后成绩是（　　）
A．43分 B．85分 C．86分 D．170分
组卷：370引用：13难度：0.9
解析
5．已知点（x₁，-3），（x₂，4）都在直线y=-2x+1上，则x₁与x₂的大小关系为（　　）
A．x₁＞x₂ B．x₁=x₂ C．x₁＜x₂ D．无法比较
组卷：422引用：3难度：0.7
解析
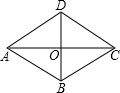6．如图，已知菱形ABCD的周长为20，对角线AC、BD交于点O，且AC+BD=14，则该菱形的面积等于（　　）
A．8 B．14 C．24 D．28
组卷：384引用：4难度：0.5
解析
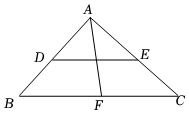7．如图，在Rt△ABC中，∠BAC=90°，D、E、F分别是三边的中点，AF=5，则DE的长为（　　）
A．2.5 B．4 C．5 D．10
组卷：204引用：6难度：0.6
解析
8．如图，在4×4的正方形网格中，每一格长度为1，小正方形的顶点称为格点，A，B，C，D，E，F都在格点上，以AB，CD，EF为边能构成一个直角三角形，则点F的位置有（　　）
A．1处 B．2处 C．3处 D．4处
组卷：662引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共9小题，共86分．解答时应写出文字说明、证明过程或演算步骤）

24．在正方形ABCD中，正方形的边长为a,点O为对角线AC的中点，点E在直线AC上，连接EB，过点E作EF⊥BE交直线AD于点F．
（1）如图1，当点E在线段AO上（不与端点重合）时，求证：∠AFE=∠ABE；
（2）如图2，当点E在线段AC上（不与端点O点重合）时，请补全图形，探究线段AB，AE，AF的数量关系并证明；
（3）若点P在射线CA上且
PC
=
2
2
a
，点E从点P运动到点C的过程中，点F随之运动，请直接写出点F运动的路径长
．（用含有a的代数式表示）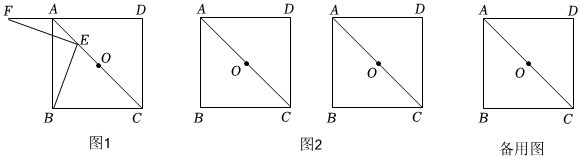
组卷：248引用：3难度：0.5
解析
25．定义：对于给定的一次函数y=kx+b（k≠0，k、b为常数），把形如
y
=
kx
+
b
（
x
≥
0
）
-
kx
+
b
（
x
＜
0
）
（k≠0，k、b为常数）的函数称为一次函数y=kx+b（k≠0，k、b为常数）的衍生函数．已知▱ABCD的顶点坐标分别为A（-2，1），B（3，1），C（5，3），D（0，3）．

（1）点E（n,3）在一次函数y=x+2的衍生函数图象上，则n=
；
（2）如图，一次函数y=kx+b（k≠0，k、b为常数）的衍生函数图象与平行四边形ABCD交于M、N、P、Q四点，其中P点坐标是（-1，2），并且
S
△
MNB
=
7
3
，求该一次函数的解析式；
（3）一次函数y=kx+b（k≠0，k、b为常数），其中k、b满足3k+b=2，它的衍生函数图象与▱ABCD恰好有两个交点，求b的取值范围．
组卷：434引用：3难度：0.3
解析