在正方形ABCD中，正方形的边长为a,点O为对角线AC的中点，点E在直线AC上，连接EB，过点E作EF⊥BE交直线AD于点F．
（1）如图1，当点E在线段AO上（不与端点重合）时，求证：∠AFE=∠ABE；
（2）如图2，当点E在线段AC上（不与端点O点重合）时，请补全图形，探究线段AB，AE，AF的数量关系并证明；
（3）若点P在射线CA上且PC=22a，点E从点P运动到点C的过程中，点F随之运动，请直接写出点F运动的路径长 4a4a．（用含有a的代数式表示）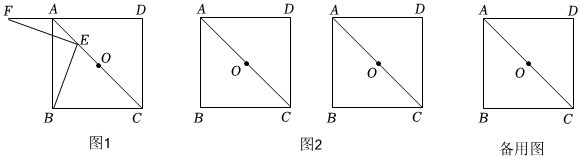
PC
=
2
2
a
【考点】四边形综合题．
【答案】4a
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：249引用：3难度：0.5
相似题
-
1．我们定义：如果两个等腰三角形的顶角相等，且顶角的顶点互相重合，则称此图形为“手拉手全等模型”．因为顶点相连的四条边，形象的可以看作两双手，所以通常称为“手拉手模型”．例如，如图（1），△ABC与△ADE都是等腰三角形，其中∠BAC=∠DAE，则△ABD≌△ACE（SAS）
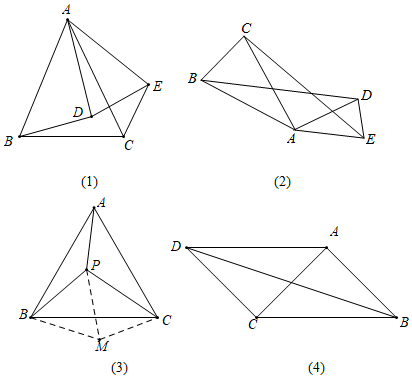
（1）熟悉模型：如图（2），已知△ABC与△ADE都是等腰三角形，AB=AC，AD=AE，且∠BAC=∠DAE，求证：BD=CE；
（2）运用模型：如图（3），P为等边△ABC内一点，且PA：PB：PC=3：4：5，求∠APB的度数．小明在解决此问题时，根据前面的“手拉手全等模型”，以BP为边构造等边△BPM，这样就有两个等边三角形共顶点B，然后连接CM，通过转化的思想求出了∠APB的度数，则∠APB的度数为度；
（3）深化模型：如图（4），在四边形ABCD中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，求BD的长．发布：2025/6/9 14:30:1组卷：2356引用：3难度：0.2 -
2．如图1．已知正方形ABCD中，BD为对角线，边长为3．E为边CD上一点，过E点作EF⊥BD于F点，
EF=2
（1）如图1．连结CF，求线段CF的长；
（2）保持△DEF不动，将正方形ABCD绕D点旋转至如图2的位置，连结BE，M点为BE的中点，连接MC、MF，探求MC与MF关系，并证明你的结论；
（3）保持△DEF不动，将正方形ABCD绕D点旋转一周，求出BE的中点M在这个过程中的运动路径长及MC的最小值．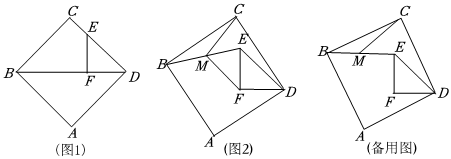
发布：2025/6/9 14:30:1组卷：559引用：5难度：0.1 -
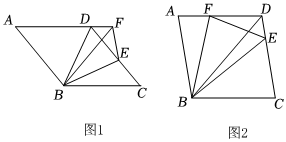3．如图1，BD是菱形ABCD的对角线，点E是边CD上一点，将△BCE沿着BE翻折，点C的对应点F恰好落在AD的延长线上，且AB=5．
（1）求证：FB平分∠AFE；
（2）如图2，若点F落在AD上．
①猜想∠ABF与∠DBE之间的数量关系，并证明你的结论；
②若，求证：EC=3DE．DFFB=23发布：2025/6/9 14:30:1组卷：155引用：3难度：0.3
