2022-2023学年浙江省绍兴市高一（下）期末数学试卷

一、单项选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知复数z在复平面内对应的点是（0，1），则

  1

  +

  i

  z

  =（　　）

  A．1+i

  B．1-i

  C．-1+i

  D．-1-i
  组卷：66引用：6难度：0.8

  解析

• 2．某组数据33、36、38、39、42、46、49、49、51、56的第80百分位数为（　　）

  A．46

  B．49

  C．50

  D．51
  组卷：87引用：6难度：0.7

  解析

• 3．已知向量

  a

  =

  （

  2

  ，

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ）

  ，则（　　）

  A． a = - 2 b

  B． a = 2 b

  C． a ∥ b

  D． a ⊥ b
  组卷：65引用：3难度：0.8

  解析

• 4．已知m,n是两条直线，α，β是两个平面，下列命题正确的是（　　）

  A．若m∥n,m∥α，则n∥α	B．若m∥β，m∥α，则α∥β
  C．若m⊥n,n⊂β，则m⊥β	D．若m∥α，m⊥β，则α⊥β
  组卷：105引用：4难度：0.8

  解析

• 5．抛掷三枚质地均匀的硬币，有如下随机事件：A_i=“正面向上的硬币数为i”，其中i=0，1，2，3，B=“恰有两枚硬币抛掷结果相同”，则下列说法正确的是（　　）

  A．A0与B相互独立	B．A3与B对立
  C．P（A2）=2P（B）	D．A1+A2=B
  组卷：89引用：3难度：0.6

  解析

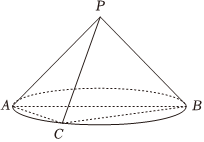• 6．轴截面为等腰直角三角形的圆锥为直角圆锥，如图所示，在直角圆锥P-ABC中，AB为底面圆的直径，C在底面圆周上且为弧

  ˆ

  AB

  的中点，则异面直线PB与AC所成角的大小为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：137引用：4难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  cos

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

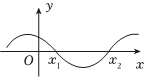  的部分图象如图所示，x₁，x₂是f（x）的两个零点，若x₂=4x₁，则下列为定值的量是（　　）

  A．φ

  B．ω

  C． φ ω

  D．ω+φ
  组卷：144引用：4难度：0.7

  解析

四、解答题（本大题共6小题，共52分.解答应写出文字说明、证明过程或演算步骤）

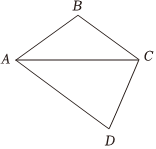• 21．如图，在平面四边形ABCD中，点B与点D分别在直线AC的两侧，BC=CD=2．
  （1）已知AB=2，且AC=AD，
  （i）当

  cos

  ∠

  CAD

  =

  2

  3

  时，求△ABC的面积；
  （ii）若

  ∠

  ABC

  =

  2

  ∠

  ADC

  ＞

  π

  2

  ，求∠ABC．
  （2）已知

  AD

  =

  2

  AB

  ，且

  ∠

  BAD

  =

  π

  4

  ，求AC的最大值．
  组卷：198引用：6难度：0.5

  解析

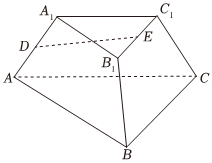• 22．如图，在正三棱台ABC-A₁B₁C₁中，AB=2A₁B₁=2AA₁，D，E分别为AA₁，B₁C₁的中点．
  （1）证明：DE⊥平面BB₁C₁C；
  （2）设P，Q分别为棱AB，BC上的点，且C₁，D，P，Q均在平面α上，若△PBQ与△ABC的面积比为3：8，
  （i）证明：BP=

  3

  4

  BA；
  （ii）求α与平面ABB₁A₁所成角的正弦值．
  组卷：201引用：4难度：0.5

  解析