2022-2023学年江西省吉安一中高二（上）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求的.

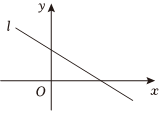• 1．已知直线l：y=xsinθ+cosθ的图像如图所示，则角θ是（　　）

  A．第一象限角

  B．第二象限角

  C．第三象限角

  D．第四象限角
  组卷：22引用：1难度：0.8

  解析

• 2．（x-y）（x+y）⁸的展开式中x³y⁶的系数为（　　）

  A．28

  B．-28

  C．56

  D．-56
  组卷：158引用：6难度：0.7

  解析

• 3．已知m,n∈R则“mn＞0”是“方程

  x

  2

  m

  +

  y

  2

  n

  =1表示的曲线是椭圆”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：92引用：3难度：0.7

  解析

• 4．两平行平面α，β分别经过坐标原点O和点A（1，2，3），且两平面的一个法向量

  n

  =

  （

  -

  1

  ，

  0

  ，

  1

  ）

  ，则两平面间的距离是（　　）

  A． 2

  B． 2 2

  C． 3

  D． 3 2
  组卷：132引用：5难度：0.7

  解析

• 5．2022​年遂宁主城区突发“920疫情”，23日凌晨2时，射洪组织五支“最美逆行医疗队”去支援遂宁主城区，将分派到遂宁船山区、遂宁经开区、遂宁高新区进行核酸采样服务，每支医疗队只能去一个区，每区至少有一支医疗队，若恰有两支医疗队者被分派到高新区，则不同的安排方法共有（　　）

  A．30种

  B．40种

  C．50种

  D．60种
  组卷：124引用：3难度：0.8

  解析

• 6．已知圆C：x²+y²-2x=0，直线l：x+y+1=0，P为l上的动点，过点P作圆C的两条切线PA、PB，切点分别A、B，当|PC|•|AB|最小时，直线PC的方程为（　　）

  A．x+y=0

  B．x-y-1=0

  C．2x-2y+1=0

  D．2x+2y+1=0
  组卷：99引用：3难度：0.6

  解析

• 7．某奥运村有A，B，C三个运动员生活区，其中A区住有30人，B区住有15人，C区住有10人．已知三个区在一条直线上，位置如图所示．奥运村公交车拟在此间设一个停靠点，为使所有运动员步行到停靠点路程总和最小，那么停靠点位置应在（　　）
  

  A．A区	B．B区
  C．C区	D．A，B两区之间
  组卷：32引用：3难度：0.8

  解析

四、解答题：本题共6小题，共0分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的右焦点F，离心率为

  1

  2

  ，且点M（1，

  3

  2

  ）在椭圆C上．
  （1）求椭圆C的标准方程；
  （2）过F的直线（不与x轴重合）与椭圆C相交于A、B两点，P不在直线AB上且

  OP

  =λ

  OA

  +（2-λ）

  OB

  ，O是坐标原点，求△PAB面积的最大值．
  组卷：40引用：2难度：0.4

  解析

• 22．如图，已知抛物线C：y²=2px（p＞0）的焦点F，且经过点A（2p,m）（m＞0），|AF|=5．
  （1）求p和m的值；
  （2）点M，N在C上，且AM⊥AN．过点A作AD⊥MN，D为垂足，证明：存在定点Q，使得|DQ|为定值．
  组卷：314引用：5难度：0.5

  解析