2023-2024学年福建省莆田四中高三(上)第一次月考数学试卷
发布:2024/8/4 8:0:9
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.设集合A={x|0≤x+1≤3},B={x|4x+3>0},则A∩B=( )
组卷:83引用:5难度:0.7 -
2.已知函数
的定义域是R,则m的取值范围是( )f(x)=1mx2+2mx+1组卷:996引用:14难度:0.5 -
3.设a∈R,则“a>1”是“a2>1”的( )
组卷:5263引用:50难度:0.9 -
4.设随机变量ξ服从正态分布N(6,σ2),若P(ξ<3a-3)=P(ξ>-a+1),则a的值为( )
组卷:188引用:3难度:0.7 -
5.若函数f(x)=x3-3x2+ax在R上是增函数,则实数a的取值范围为( )
组卷:343引用:4难度:0.6 -
6.已知函数
,若f(t)=4,则f(-t)=( )f(x)=ax3+bx+cx+3组卷:484引用:3难度:0.8 -
7.设
,则a,b,c的大小关系为( )a=30.7,b=(13)-0.8,c=log0.70.8组卷:136引用:6难度:0.8
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
-
21.放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节,运行效率不断提升.以下是根据近10年年份数xi与该机场飞往A地航班放行准点率yi(i=1,2,…,10)(单位:百分比)的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
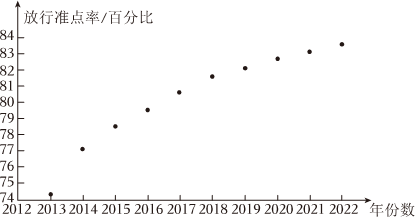
其中ti=ln(xi-2012),xyt10∑i=1x2i10∑i=1xiyi10∑i=1t2i10∑i=1tiyi2017.5 80.4 1.5 40703145.0 1621254.2 27.7 1226.8 t=11010∑i=1ti
(1)根据散点图判断,y=bx+a与y=cln(x-2012)+d哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型(给出判断即可,不必说明理由),并根据表中数据建立经验回归方程,由此预测2023年该机场飞往A地的航班放行准点率.
(2)已知2023年该机场飞往A地、B地和其他地区的航班比例分别为0.2、0.2和0.6.若以(1)中的预测值作为2023年该机场飞往A地航班放行准点率的估计值,且2023年该机场飞往B地及其他地区(不包含A、B两地)航班放行准点率的估计值分别为80%和75%,试解决以下问题:
(i)现从2023年在该机场起飞的航班中随机抽取一个,求该航班准点放行的概率;
(ii)若2023年某航班在该机场准点放行,判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大,说明你的理由.
附:(1)对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为,̂β=n∑i=1(ui-u)(vi-v)n∑i=1(ui-u)2=n∑i=1uivi-nuvn∑i=1u2i-nu2̂α=v-̂βu
参考数据:ln10≈2.30,ln11≈2.40,ln12≈2.48.组卷:562引用:7难度:0.6 -
22.已知函数f(x)=ax2+lnx(a∈R)有最大值
,g(x)=x2-2x+f(x),且g'(x)是g(x)的导数.-12
(Ⅰ)求a的值;
(Ⅱ)证明:当x1<x2,g(x1)+g(x2)+3=0时,.g′(x1+x2)>12组卷:264引用:5难度:0.1


