2022-2023学年山东省枣庄市市中三中高二（下）月考数学试卷（5月份）
发布：2024/7/21 8:0:9
一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
-
1．某班周一上午共有四节课，计划安排语文、数学、美术、体育各一节，要求体育不排在第一节，美术不排在第四节，则该班周一上午不同的排课方案共有（ ）
组卷：44引用：2难度：0.7 -
2．某试验每次成功的概率为p（0＜p＜1），现重复进行9次该试验，则恰好有2次试验未成功的概率为（ ）
组卷：35引用：2难度：0.7 -
3．已知随机变量ξ服从正态分布N（3，σ2），且P（0＜ξ＜3）=0.4，则P（ξ＞6）=（ ）
组卷：73引用：2难度：0.8 -
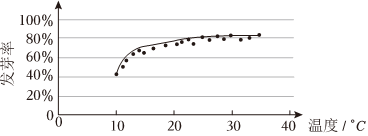4．某校一个课外学习小组为研究某作物种子的发芽率y和温度x（单位：℃）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据（xi，yi）（i=1，2，…，20）得到下面的散点图：
由此散点图，在10℃至35℃之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是（ ）组卷：66引用：2难度：0.8 -
5．若
展开式的常数项等于-280，则a=（ ）（x+2）（1x-ax）7组卷：211引用：4难度：0.8 -
6．从1，2，3，4，5，6，7，8，9，10中不放回地依次取2个数，事件A为“第一次取到的是偶数”，事件B为“第二次取到的是3的整数倍”，则P（B|A）=（ ）
组卷：231引用：3难度：0.5 -
7．设n∊N+，则5
+52C1n+53C2n+…+5nC3n除以7的余数为（ ）Cnn组卷：406引用：7难度：0.9
四、解答题：本大题共6小题，共70分．
-
21．已知函数
．f（x）=ex-lnxx-1
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若函数有两个零点x1，x2（其中x1＜x2），求实数a的取值范围．g（x）=f（x）-ax组卷：37引用：2难度：0.4 -
22．某医疗机构，为了研究某种病毒在人群中的传播特征，需要检测血液是否为阳性．若现有n（n∈N*）份血液样本，每份样本被取到的可能性相同，检测方式有以下两种：
方式一：逐份检测，需检测n次；
方式二：混合检测，将其中k（k∈N*，k≥2）份血液样本分别取样混合在一起检测，若检测结果为阴性，说明这k份样本全为阴性，则只需检测1次；若检测结果为阳性，则需要对这k份样本逐份检测，因此检测总次数为k+1次．假设每份样本被检测为阳性或阴性是相互独立的，且每份样本为阳性的概率是p（0＜p＜1）．
（1）在某地区，通过随机检测发现该地区人群血液为阳性的概率约为0.8%．为了调查某单位该病毒感染情况，随机选取50人进行检测，有两个分组方案：
方案一：将50人分成10组，每组5人；
方案二：将50人分成5组，每组10人．
试分析哪种方案的检测总次数更少？（取0.9925=0.961，0.99210=0.923，0.99211=0.915）
（2）现取其中k份血液样本，若采用逐份检验方式，需要检测的总次数为ξ1；采用混合检测方式，需要检测的总次数为ξ2．若E（ξ1）=E（ξ2），试解决以下问题：
①确定p关于k的函数关系；
②当k为何值时，p取最大值并求出最大值．组卷：105引用：4难度：0.4
