某医疗机构,为了研究某种病毒在人群中的传播特征,需要检测血液是否为阳性.若现有n(n∈N*)份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:
方式一:逐份检测,需检测n次;
方式二:混合检测,将其中k(k∈N*,k≥2)份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这k份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这k份样本逐份检测,因此检测总次数为k+1次.假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是p(0<p<1).
(1)在某地区,通过随机检测发现该地区人群血液为阳性的概率约为0.8%.为了调查某单位该病毒感染情况,随机选取50人进行检测,有两个分组方案:
方案一:将50人分成10组,每组5人;
方案二:将50人分成5组,每组10人.
试分析哪种方案的检测总次数更少?(取0.9925=0.961,0.99210=0.923,0.99211=0.915)
(2)现取其中k份血液样本,若采用逐份检验方式,需要检测的总次数为ξ1;采用混合检测方式,需要检测的总次数为ξ2.若E(ξ1)=E(ξ2),试解决以下问题:
①确定p关于k的函数关系;
②当k为何值时,p取最大值并求出最大值.
【考点】离散型随机变量的均值(数学期望).
【答案】(1)方案二;
(2)①p=1-,(k≥2,k∈N*);
②k=3,p=1-.
(2)①p=1-
(
1
k
)
1
k
②k=3,p=1-
(
1
3
)
1
3
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/21 8:0:9组卷:107引用:4难度:0.4
相似题
-
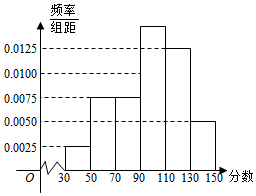 1.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
1.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间(110,150]的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间(110,130]与(130,150]各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的7人中,选出3人参加全市座谈交流,设X表示得分在区间(130,150]中参加全市座谈交流的人数,求X的分布列及数学期望E(X).发布:2024/12/29 13:30:1组卷:134引用:7难度:0.5 -
2.设离散型随机变量X的分布列如表:
若离散型随机变量Y=-3X+1,且E(X)=3,则( )X 1 2 3 4 5 P m 0.1 0.2 n 0.3 发布:2024/12/29 13:0:1组卷:199引用:6难度:0.5 -
3.从4名男生和2名女生中任选3人参加演讲比赛,用X表示所选3人中女生的人数,则E(X)为( )
发布:2024/12/29 13:30:1组卷:139引用:6难度:0.7


