2023-2024学年北京交大附中高三（上）诊断数学试卷（10月份）

一、选择题。（每小题4分，共40分）

• 1．已知全集U=R，集合A={x|-2≤x≤3}，B={x|x＜-1或x＞4}，那么集合A∩（∁_UB）等于（　　）

  A．{x|-2≤x≤4}

  B．{x|x≤3或x≥4}

  C．{x|-2≤x＜-1}

  D．{x|-1≤x≤3}
  组卷：750引用：37难度：0.9

  解析

• 2．已知向量

  a

  =（m,2），

  b

  =（2，-1）．若

  a

  ∥

  b

  ，则m的值为（　　）

  A．4

  B．1

  C．-4

  D．-1
  组卷：252引用：7难度：0.9

  解析

• 3．命题p：∀x＞2，x²-1＞0，则￢p是（　　）

  A．∀x＞2，x2-1≤0	B．∀x≤2，x2-1＞0
  C．∃x＞2，x2-1≤0	D．∃x≤2，x2-1≤0
  组卷：422引用：61难度：0.9

  解析

• 4．已知函数f（x）=lnx+x-4，在下列区间中，包含f（x）零点的区间是（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  组卷：502引用：8难度：0.7

  解析

• 5．为了得到函数

  y

  =

  -

  sin

  （

  x

  -

  π

  3

  ）

  的图象，只需把函数y=sinx的图象上的所有点（　　）

  A．向左平移 2 π 3 个单位长度

  B．向左平移 π 3 个单位长度

  C．向右平移 π 3 个单位长度

  D．向右平移 5 π 3 个单位长度
  组卷：467引用：3难度：0.7

  解析

• 6．在△ABC中，

  B

  =

  π

  4

  ，

  AC

  =

  2

  ，则“

  BC

  =

  3

  ”是“

  A

  =

  π

  3

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：100引用：1难度：0.6

  解析

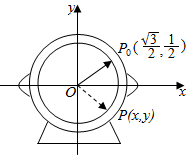• 7．如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置p（x,y）．若初始位置为P₀（

  3

  2

  ，

  1

  2

  ），当秒针从P₀（注此时t=0）正常开始走时，那么点P的纵坐标y与时间t的函数关系为（　　）

  A．y=sin（ π 30 t + π 6 ）	B． y = sin （ - π 60 t - π 6 ）
  C．y=sin（- π 30 t + π 6 ）	D．y=sin（- π 30 t - π 3 ）
  组卷：1554引用：30难度：0.7

  解析

三、解答题。（共85分）

• 20．已知函数f（x）=

  1

  2

  x²-x+alnx,（a＞0）．
  （1）若a=1，求f（x）在（1，f（1））处的切线方程；
  （2）讨论f（x）的单调性；
  （3）若f（x）存在两个极值点x₁，x₂，求证：f（x₁）+f（x₂）＞

  -

  3

  -

  2

  ln

  2

  4

  ．
  组卷：1279引用：5难度：0.3

  解析

• 21．设集合S={a₁，a₂，…a_n}（n≥3），其中

  a

  i

  ∈

  N

  *

  ，i=1，2，…，n.若集合S满足对于任意的两个非空集合A，B⊆S，都有集合A的所有元素之和与集合B的元素之和不相等，则称集合S具有性质P．
  （1）判断集合{1，2，3，5，9}，{1，3，5，11}是否具有性质P，并说明理由；
  （2）若集合

  S

  =

  {

  a

  1

  ，

  a

  2

  ，

  ⋯

  ，

  a

  n

  }

  （

  n

  ∈

  N

  *

  ）

  具有性质P，求证：∀k≤n,

  a

  1

  +

  a

  2

  +

  ⋯

  +

  a

  k

  ≥

  2

  k

  -

  1

  ，

  k

  ∈

  N

  *

  ；
  （3）若集合S={a₁，a₂，…，a₂₀₂₃}具有性质P，求

  1

  a

  1

  +

  1

  a

  2

  +

  ⋯

  +

  1

  a

  2023

  的最大值．
  组卷：56引用：1难度：0.5

  解析