2021-2022学年吉林省长春外国语学校九年级（下）期初数学试卷

一、选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．比-2小的数是（　　）

  A．-1

  B．-3

  C．0

  D．- 1 2
  组卷：7引用：1难度：0.9

  解析

• 2．据统计，2022年春运全国铁路累计发送旅客约2300000000人次，2300000000这个数用科学记数法表示为（　　）

  A．0.23×109

  B．2.3×1010

  C．2.3×109

  D．23×108
  组卷：19引用：3难度：0.8

  解析

• 3．下列四个几何体的俯视图中与众不同的是（　　）

  A．

  B．

  C．

  D．
  组卷：483引用：16难度：0.9

  解析

• 4．不等式3x-6＞0的解集为（　　）

  A．x＞2

  B．x≥2

  C．x＜2

  D．x≤2
  组卷：81引用：1难度：0.8

  解析

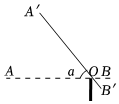• 5．如图，某停车场入口的栏杆AB，从水平位置绕点O旋转到A′B′的位置，已知AO的长为4米．若栏杆的旋转角∠AOA′=α，则栏杆A端升高的高度为（　　）

  A． 4 sinα 米

  B．4sinα米

  C． 4 cosα 米

  D．4cosα米
  组卷：2420引用：33难度：0.8

  解析

• 6．如图，AB∥CD，直线EF分别交AB、CD于M、N两点，将一个含有45°的直角三角尺按如图所示的方式摆放，若∠EMB=80°，则∠PNM的度数是（　　）

  A．30°

  B．45°

  C．20°

  D．35°
  组卷：17引用：1难度：0.7

  解析

• 7．如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．
  步骤1：以C为圆心，CA为半径画弧①；
  步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
  步骤3：连接AD，交BC延长线于点H．
  下列叙述正确的是（　　）

  A．S△ABC=BC•AH	B．AC平分∠BAD
  C．BH垂直平分线段AD	D．AB=AD
  组卷：515引用：8难度：0.5

  解析

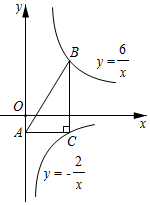• 8．如图，点B在反比例函数y=

  6

  x

  （x＞0）的图象上，点C在反比例函数y=-

  2

  x

  （x＞0）的图象上，且BC∥y轴，AC⊥BC，垂足为点C，交y轴于点A．则△ABC的面积为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：3421引用：26难度：0.6

  解析

三、解答题（本大题共10小题，共58分.解答应写出必要的文字说明、证明过程或演算步骤）

• 23．如图所示，在Rt△ABC中，∠B=90°，AB=6cm,CB=3cm,点P在AC上以

  5

  cm/s的速度从点A匀速运动至点C停止，点Q沿BA方向以2cm/s的速度运动，当点P不与点A重合时，连结PQ，以PQ、BQ为邻边作平行四边形PQBM，当P点停止运动时，点Q也随之停止运动，设点P的运动时间为t（s）．
  （1）AC=

  ；
  （2）当四边形PQBM为矩形时，求t的值；
  （3）当△PQM是钝角三角形时，求t的取值范围．
  组卷：22引用：1难度：0.1

  解析

• 24．在平面直角坐标系中，抛物线的解析式为y=-x²+（n-1）x+n.
  （1）当n=3时，求抛物线所对应的函数表达式及顶点坐标；
  （2）当抛物线的顶点到x轴的距离为2时，求n的值；
  （3）已知线段AB的两个端点坐标分别为A（-6，-2），B（3，-2），当抛物线与线段有一个交点时，直接写出n的取值范围．
  组卷：79引用：1难度：0.4

  解析