2022-2023学年广东省珠海市高二（下）期末数学试卷

一、选择题：本题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．

  A

  3

  5

  -

  C

  2

  4

  =（　　）

  A．66

  B．54

  C．26

  D．14
  组卷：64引用：2难度：0.7

  解析

• 2．已知离散型随机变量ξ的分布列如下表，则其数学期望E（ξ）=（　　）
  

  ξ	1	2	4
  P	0.2	m	0.6

  A．1

  B．0.2

  C．2.8

  D．3
  组卷：46引用：3难度：0.5

  解析

• 3．已知等差数列{a_n}的前n项和为S_n，且a₂+a₆=12，S₄=18，则a₃=（　　）

  A．5

  B．4

  C．3

  D．2
  组卷：115引用：1难度：0.7

  解析

• 4．在杨辉三角中，每一个数值是它肩上面两个数值之和．这个三角形开头几行如图，若第n行从左到右第12个数与第13个数的比值为2，则n=（　　）

  A．15

  B．16

  C．17

  D．18
  组卷：22引用：1难度：0.8

  解析

• 5．下列导数运算正确的是（　　）

  A．（cosx）′=sinx	B． （ lo g 2 x ） ′ = 1 x • ln 2
  C．（2x）′=2x	D． （ 1 x ） ′ = 1 x 2
  组卷：94引用：3难度：0.9

  解析

• 6．已知等比数列{a_n}的前n项和为S_n，且S_n=λ•2ⁿ-2，则λ=（　　）

  A．4

  B．3

  C．2

  D．1
  组卷：166引用：4难度：0.8

  解析

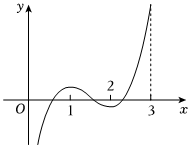• 7．已知定义在（0，3]上的函数f（x）的图象如图，则不等式（x-1）•f'（x）＜0的解集为（　　）

  A．（0，2）	B．（1，2）
  C．（2，3）	D．（0，1）∪（1，2）
  组卷：126引用：5难度：0.6

  解析

四、解答题：本题共6个小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．设有甲、乙、丙三个不透明的箱子，每个箱中装有除颜色外其他都相同的四个球，其中甲箱有两个黄球和两个黑球，乙箱有三个红球和一个白球，丙箱有两个红球和两个白球．完成以下步骤称为一次“操作”：先一次从甲箱中随机摸出两个球，若从甲箱中摸出的两个球同色，则从乙箱中随机摸出一个球放入丙箱，再一次从丙箱中随机摸出两个球；若从甲箱中摸出的两个球不同色，则从丙箱中随机摸出一个球放入乙箱，再一次从乙箱中随机摸出两个球．
  （1）求一次“操作”完成后，最后摸出的两个球均为白球的概率；
  （2）若一次“操作”最后摸出的两个球均为白球，求这两个球是从丙箱中摸出的概率；
  （3）若摸出每个红球记1分，摸出每个白球记-2分．用X表示一次“操作”完成后，最后摸到的两个球的分数之和，求X的分布列及数学期望．
  组卷：50引用：1难度：0.5

  解析

• 22．已知函数f（x）=2ln（x+1）+a（x-1）²，其中a为常数．
  （1）若a=-1，求函数f（x）在其定义域内的单调区间；
  （2）证明：对任意n∈N^*，都有：

  2

  n

  -

  1

  n

  2

  ＜

  2

  ln

  1

  +

  n

  n

  ；
  （3）证明：对任意n∈N^*，都有：

  1

  +

  3

  2

  2

  +

  5

  3

  2

  +

  …

  +

  2

  n

  -

  1

  n

  2

  ＜

  2

  n

  n

  +

  1

  ．
  组卷：63引用：3难度：0.5

  解析