2022-2023学年福建省厦门一中海沧校区高一（下）月考数学试卷（6月份）

一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．若复数z₁，z₂在复平面内对应的点关于x轴对称，且z₁=1+i,则复数

  z

  2

  z

  1

  =（　　）

  A．1

  B．-1

  C．i

  D．-i
  组卷：104引用：6难度：0.7

  解析

• 2．为了提高学习兴趣，某数学老师把《九章算术》与《孙子算经》这两本数学著作推荐给学生进行课外阅读，若该班甲、乙两名同学每人至少阅读其中的一本，则每本书都被同学阅读的概率为（　　）

  A． 2 9

  B． 1 3

  C． 2 3

  D． 7 9
  组卷：30引用：3难度：0.7

  解析

• 3．抛掷两枚质地均匀的硬币，设事件A=“第一枚硬币正面朝上”，事件B=“第二枚硬币反面朝上”，则下列说法正确的是（　　）

  A．A与B互为对立事件	B．P（A）=P（B）
  C．A与B相等	D．A与B互斥
  组卷：486引用：10难度：0.7

  解析

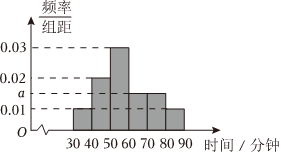• 4．为了解“双减”政策实施后学生每天的体育活动时间，研究人员随机调查了该地区1000名学生每天进行体育运动的时间，按照时长（单位：分钟）分成6组：第一组[30，40），第二组[40，50），第三组[50，60），第四组[60，70），第五组[70，80），第六组[80，90]，经整理得到如图的频率分布直方图，则可以估计该地区学生每天体育活动时间的第70百分位数位于的区间为（　　）

  A．[50，60）

  B．[60，70）

  C．[70，80）

  D．[80，90]
  组卷：35引用：1难度：0.7

  解析

• 5．在△ABC中，角A，B，C所对边分别为a,b,c,cosA（2sinB-sinC）=sinAcosC，则A的值为（　　）

  A． π 6

  B． π 2

  C． π 3

  D． 2 π 3
  组卷：62引用：2难度：0.7

  解析

• 6．在三角形ABC中，AB=7，BC=8，AC=9，AM和AN分别是BC边上的高和中线，则

  MN

  •

  BC

  =（　　）

  A．14

  B．15

  C．16

  D．17
  组卷：100引用：3难度：0.6

  解析

• 7．已知平面向量

  a

  ，

  b

  ，

  c

  ．满足|

  a

  |=2，|

  a

  -

  b

  |=2

  3

  ，若对于任意实数x都有|

  b

  -x

  a

  |≥|

  b

  -

  a

  |成立，且|

  c

  -

  a

  |≤1，则

  b

  •

  c

  的最大值为（　　）

  A．2

  B．4

  C．6

  D．8
  组卷：228引用：4难度：0.5

  解析

四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．

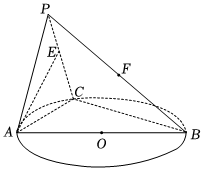• 21．如图，C是以AB为直径的圆O上异于A，B的点，平面PAC⊥平面ABC，△PAC为正三角形，E，F分别是PC，PB上的动点．
  （1）求证：BC⊥AE；
  （2）若E，F分别是PC，PB的中点且异面直线AF与BC所成角的正切值为

  3

  2

  ，记平面AEF与平面ABC的交线为直线l,点Q为直线l上动点，求直线PQ与平面AEF所成角的取值范围．
  组卷：303引用：9难度：0.6

  解析

• 22．十字测天仪广泛应用于欧洲中世纪晚期的航海领域，主要用于测量太阳等星体的方位，便于船员确定位置．如图1所示，十字测天仪由杆AB和横档CD构成，并且E是CD的中点，横档与杆垂直并且可在杆上滑动．十字测天仪的使用方法如下：如图2，手持十字测天仪，使得眼睛可以从A点观察．滑动横档CD使得A，C在同一水平面上，并且眼睛恰好能观察到太阳，此时视线恰好经过点D，DE的影子恰好是AE．然后，通过测量AE的长度，可计算出视线和水平面的夹角∠CAD（称为太阳高度角），最后通过查阅地图来确定船员所在的位置．
  
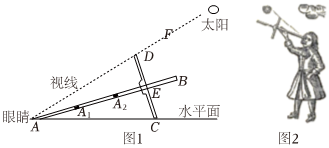
  （1）若在某次测量中，横档CD的长度为20，测得太阳高度角∠CAD=60°，求影子AE的长；
  （2）若在另一次测量中，AE=40，横档CD的长度为20，求太阳高度角的正弦值；
  （3）在杆AB上有两点A₁，A₂满足AA₁=

  1

  2

  A

  A

  2

  ．当横档CD的中点E位于A_i时，记太阳高度角为a_i（i=1，2），其中α₁，α₂都是锐角．证明：α₁＜2α₂．
  组卷：87引用：6难度：0.5

  解析