当前位置：试卷中心 > 试卷详情

2023年江苏省连云港外国语学校中考数学二模试卷

发布：2024/6/24 8:0:9

一、选择题（本大题共8小题，每小题3分，共24分）

1．下列运算正确的是（　　）
A．a²+a³=a⁵ B．（a²）³=a⁵
C．a⁶÷a³=a² D．（ab²）³=a³b⁶
组卷：383引用：8难度：0.8
解析
2．29的算术平方根介于（　　）
A．6与7之间 B．5与6之间 C．4与5之间 D．3与4之间
组卷：206引用：3难度：0.8
解析
3．每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为0.0000105m,该数值用科学记数法表示为（　　）
A．0.105×10^-6 B．1.05×10^-5 C．1.05×10^-6 D．10.5×10^-7
组卷：49引用：2难度：0.8
解析
4．分别观察下列几何体，其中主视图、左视图和俯视图完全相同的是（　　）
A．
圆锥 B．
圆柱 C．
三棱柱 D．
正方体
组卷：1570引用：29难度：0.8
解析
5．关于二次函数y=-（x+1）²+2的图象，下列判断正确的是（　　）
A．图象开口向上
B．图象的对称轴是直线x=1
C．图象有最低点
D．图象的顶点坐标为（-1，2）
组卷：1541引用：7难度：0.9
解析
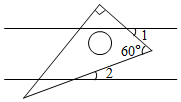6．如图，将一块含有60°角的直角三角板放置在两条平行线上，若∠1=45°，则∠2为（　　）
A．15° B．25° C．35° D．45°
组卷：1618引用：13难度：0.6
解析
7．如图，在平行四边形ABCD中，E为BC的中点，BD，AE交于点O，若随机向平行四边形ABCD内投一粒米，则米粒落在图中阴影部分的概率为（　　）
A．
1
16
B．
1
12
C．
1
8
D．
1
6
组卷：1510引用：10难度：0.5
解析
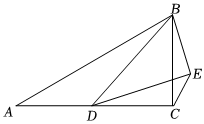8．如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，AC=4，点D是边AC上一动点，连接BD，以BD为斜边作Rt△BDE，使∠BDE=30°，∠BED=90°，连接CE．则△CDE面积的最大值（　　）
A．
4
5
B．
3
2
C．
5
3
D．
5
6
组卷：933引用：4难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10题，满分共102分）

25．“关联”是解决数学问题的重要思维方式．角平分线的有关联想就有很多……
【问题提出】
（1）如图①，PC是△PAB的角平分线，求证：
PA
PB
=
AC
BC
．

小明思路：关联“平行线、等腰三角形”，过点B作BD∥PA，交PC的延长线于点D，利用“三角形相似”．
小红思路：关联“角平分线上的点到角的两边的距离相等”，过点C分别作CD⊥PA交PA于点D，作CE⊥PB交PB于点E，利用“等面积法”．

请根据小明或小红的思路，选择一种并完成证明．
【理解应用】
（2）如图②，在Rt△ABC中，∠BAC=90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，使点C恰好落在边AB上的E点处，落AC=1，AB=2，则DE的长为
．
【深度思考】
（3）如图③，△ABC中，AB=6，AC=4，AD为∠BAC的角平分线．AD的垂直平分线EF交BC延长线于点F，连接AF，当BD=3时，AF的长为
．
【拓展升华】
（4）如图④，PC是△PAB的角平分线，若AC=3，BC=1，则△PAB的面积最大值是
．

组卷：798引用：4难度：0.5

解析

26．在平面直角坐标系中，抛物线y=ax²+bx+c与x轴交于点A（-1，0）和点B，与y轴交于点C，顶点D的坐标为（1，-4）．
（1）求出抛物线的解析式；
（2）如图1．若点P在抛物线上且满足∠PCB=∠CBD，求点P的坐标；
（3）如图2．M是直线BC上一个动点，过点M作MN⊥x轴交抛物线于点N，Q是直线AC上一个动点，当△QMN为等腰直角三角形时，直接写出此时点M的坐标．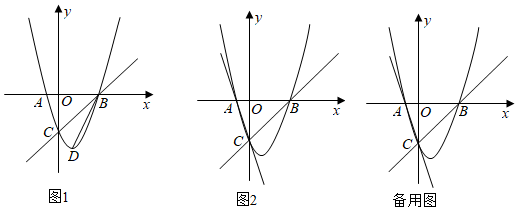
组卷：593引用：2难度：0.4
解析