当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省苏州市常熟中学高一（下）调研数学试卷（5月份）

发布：2024/5/25 8:0:9

一、单项选择题：本题共8小题，每小题5分，共40分．

1．复数z=（1-i）i的虚部是（　　）
A．i B．-i C．-1 D．1
组卷：101引用：7难度：0.9
解析
2．设a,b,c为不同的直线，α，β，γ为不同的平面，则下列结论中正确的个数为（　　）
①若a∥b,b∥c,则a∥c；
②若a∥α，b∥α，则a∥b；
③若a∥β，a⊂α，α∩β=b,则a∥b；
④若a∥b,a∥α，则b∥α．
A．1 B．2 C．3 D．4
组卷：99引用：1难度：0.7
解析
3．设
a
，
b
是两个不共线的非零向量，则“
a
+
λ
b
与
λ
a
+
4
b
共线”是“λ=2”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：307引用：3难度：0.7
解析
4．若一个圆锥的母线长为4，且其侧面积为其轴截面面积的4倍，则该圆锥的高为（　　）
A．π B．
3
π
2
C．
2
π
3
D．
π
2
组卷：417引用：7难度：0.8
解析
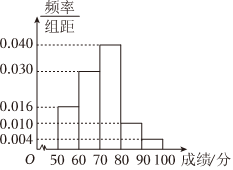5．如图是根据某班学生在一次体能素质测试中的成绩画出的频率分布直方图，则由直方图得到的80%分位数为（　　）
A．75 B．77.5 C．78 D．78.5
组卷：151引用：4难度：0.7
解析
6．已知cos（
α
-
π
6
）=
3
4
，则sin（2
α
+
π
6
）+cos²（
α
2
-
π
12
）的值为（　　）
A．
1
4
B．
1
2
C．
3
7
8
D．1
组卷：745引用：11难度：0.7
解析
7．已知正方体ABCD-A₁B₁C₁D₁中，点M在线段CC₁上，记平面BDM∩平面B₁D₁M=l,则异面直线AB₁与直线l所成角为（　　）
A．
π
6
B．
π
4
C．
π
3
D．
π
2
组卷：49引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．

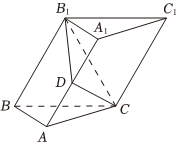21．如图，在斜三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=AC，侧面BB₁C₁C为菱形，且∠B₁BC=60°，点D为棱A₁A的中点，DB₁=DC，平面B₁CD⊥平面BB₁C₁C．
（Ⅰ）若
BB
1
=
2
，
CD
=
2
，求三棱锥D-B₁BC的体积；
（Ⅱ）设平面B₁CD与平面ABC的交线为l,求证：l⊥平面BB₁C₁C．
组卷：200引用：4难度：0.6
解析
22．如图，在我校即将投入使用的新校门旁修建了一条专门用于跑步的红色跑道，这条跑道一共由三个部分组成，其中第一部分为曲线段ABCD，该曲线段可近似看作函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），x∈[-4，0]的图象，图象的最高点坐标为C（-1，2）．第二部分是长为1千米的直线段DE，DE∥x轴．跑道的最后一部分是以O为圆心的一段圆弧
ˆ
EF
．
（1）若新校门位于图中的B点，其离AF的距离为1千米，一学生准备从新校门笔直前往位于O点的万象楼，求该学生走过的路BO的长；
（2）若点P在弧
ˆ
EF
上，点M和点N分别在线段OF和线段OE上，若平行四边形OMPN区域为学生的休息区域，记∠POF=θ，请写出学生的休息区域OMPN的面积S关于θ的函数关系式，并求当θ为何值时，S取得最大值．
组卷：192引用：8难度：0.5
解析