2023年浙江省湖州市南浔区中考数学二模试卷

一、选择题（本题有10小题，每小题3分，共30分）

• 1．2的倒数是（　　）

  A．- 1 2

  B．-2

  C． 1 2

  D．2
  组卷：975引用：44难度：0.9

  解析

• 2．计算（-3）×2的结果是（　　）

  A．-6

  B．-1

  C．1

  D．6
  组卷：1429引用：16难度：0.7

  解析

• 3．若分式

  x

  +

  2

  x

  -

  3

  的值为0，则x的值为（　　）

  A．x=-2

  B．x=0

  C．x=2

  D．x=3
  组卷：342引用：5难度：0.7

  解析

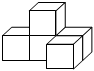• 4．如图所示的几何体的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：187引用：4难度：0.8

  解析

• 5．一组数据：7，5，8，7，9．这组数据的众数是（　　）

  A．5

  B．7

  C．8

  D．9
  组卷：73引用：4难度：0.8

  解析

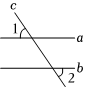• 6．如图，直线a,b被直线c所截，且a∥b.若∠1=50°，则∠2=（　　）
  

  A．40°

  B．45°

  C．50°

  D．55°
  组卷：73引用：2难度：0.8

  解析

• 7．已知平面内有⊙O与直线AB，⊙O的半径为3cm,点O到直线AB的距离为3cm,则直线AB与⊙O的位置关系是（　　）

  A．相切

  B．相交

  C．相离

  D．不能判断
  组卷：261引用：3难度：0.5

  解析

• 8．如图，在△ABC中，BA=BC，∠B=80°，按下列步骤作图：
  ①以点C为圆心，适当长度为半径作圆弧，与CA，BC延长线分别交于M，N两点；
  ②分别以M，N为圆心，大于

  1

  2

  MN

  长为半径作圆弧，两条圆弧交于点D；
  ③过点C，D作射线CD．则∠DCN的度数为（　　）
  

  A．60°

  B．65°

  C．70°

  D．75°
  组卷：62引用：1难度：0.6

  解析

三、解答题（本题有8小题，共66分）

• 23．定义：如果四边形的一条对角线把该四边形分割成两个等腰三角形，且这条对角线是这两个等腰三角形的腰，那么我们称这个四边形为双等腰四边形．
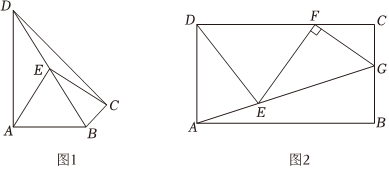
  （1）如图1，在四边形ABCD中，∠BAD=∠BCD=90°，连结BD，点E是BD的中点，连结AE，CE．
  ①试判断四边形ABCE是否是双等腰四边形，并说明理由；
  ②若∠AEC=90°，求∠ABC的度数；
  （2）如图2，点E是矩形ABCD内一点，点F是边CD上一点，四边形AEFD是双等腰四边形，且AD=DE．延长AE交BC于点G，连结FG．若AD=5，∠EFG=90°，

  CG

  FC

  =

  3

  4

  ，求AB的长．
  组卷：168引用：1难度：0.1

  解析

• 24．如图，已知在等腰△ABC中，AB=AC=5，

  BC

  =

  4

  5

  ，M是AC的中点，D，E分别是线段AM，BC上的两个动点，且满足

  BE

  =

  2

  5

  5

  CD

  ，连接DE，以点E为旋转中心，将线段ED顺时针旋转90°后得到线段EF，连接DF，△DEF的外接圆⊙O交BC于点G，连接DG．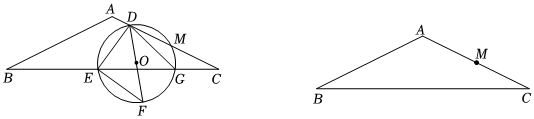
  
  （1）求sinC的值；
  （2）设CD的长为m,△DEG面积为S．
  ①求S关于m的函数关系式；
  ②在点D，E的运动过程中，求S的取值范围．
  组卷：90引用：2难度：0.4

  解析