2022年北京171中高考数学三模试卷

一、选择题（共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项）

• 1．已知集合A={x|x＜1}，B={x|0≤x≤2}，则A∩B=（　　）

  A．{x|0≤x＜1}

  B．{x|1＜x≤2}

  C．{x|x＜1}

  D．{x|x≤2}
  组卷：98引用：3难度：0.8

  解析

• 2．在复平面内，复数

  z

  =

  1

  -

  3

  i

  1

  +

  i

  ，则

  z

  对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：94引用：2难度：0.8

  解析

• 3．在公差不为零的等差数列{a_n}中，若3a_m=a₁+a₂+a₃，则m=（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：392引用：2难度：0.7

  解析

• 4．下列函数中最小正周期不是π的周期函数为（　　）

  A．y=sin|x|

  B．y=|sinx|

  C．y=cos|x|

  D．y=|tanx|
  组卷：371引用：2难度：0.7

  解析

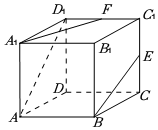• 5．如图，在正方体ABCD-A₁B₁C₁D₁中，E，F分别为CC₁，D₁C₁的中点，则下列直线中与直线BE相交的是（　　）

  A．直线A1F

  B．直线AD1

  C．直线C1D1

  D．直线AA1
  组卷：280引用：3难度：0.8

  解析

• 6．已知直线

  y

  =

  k

  （

  x

  -

  3

  ）

  与圆O：x²+y²=4交于A，B两点，且OA⊥OB，则k=（　　）

  A． 2

  B． ± 2

  C．1

  D．±1
  组卷：341引用：3难度：0.6

  解析

• 7．若某地区60岁及以上人群的新冠疫苗全程（两针）接种率为60%，加强免疫接种（第三针）的接种率为36%，则在该地区完成新冠疫苗全程接种的60岁及以上人群中随机抽取一人，此人完成了加强免疫接种的概率为（　　）

  A．0.6

  B．0.375

  C．0.36

  D．0.216
  组卷：136引用：2难度：0.9

  解析

三、解答题（共6道大题，共85分）

• 20．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左焦点为F₁（-2，0），长轴长为

  2

  6

  ．过右焦点F₂的直线l交椭圆C于A，B两点，直线F₁A，F₁B分别交直线x=3于点M，N．
  （Ⅰ）求椭圆C的方程；
  （Ⅱ）设线段AB中点为T，当点M，N位于x轴异侧时，求T到直线x=3的距离的取值范围．
  组卷：268引用：2难度：0.6

  解析

• 21．已知无穷数列A：a₁，a₂，⋯满足：
  ①

  a

  i

  ∈

  N

  *

  （

  i

  =

  1

  ，

  2

  ，

  ⋯

  ）

  ；
  ②a_i+a_j≤a_i+j≤a_i+a_j+1（i=1，2，⋯；j=1，2，⋯；i+j≥3）．
  设

  a

  *

  i

  为a_i（i=1，2，⋯）所能取到的最大值，并记数列

  A

  *

  ：

  a

  *

  1

  ，

  a

  *

  2

  ，

  ⋯

  ．
  （Ⅰ）若a₁=1，写出一个符合条件的数列A的通项公式；
  （Ⅱ）若a₁=a₂=1，求

  a

  *

  4

  的值；
  （Ⅲ）若a₁=1，a₂=2，求数列A^*的前100项和．
  组卷：95引用：3难度：0.2

  解析