当前位置：试卷中心 > 试卷详情

2023-2024学年河南省信阳市固始县桃花坞中学及分校八年级（上）开学数学试卷

发布：2024/8/15 5:0:1

一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的.

1．已知三角形的两边长分别为4和9，则此三角形的第三边长可能为（　　）
A．9 B．4 C．5 D．13
组卷：1257引用：13难度：0.4
解析
2．将一个n边形变成（n+2）边形，内角和将（　　）
A．减少180° B．增加180° C．减少360° D．增加360°
组卷：730引用：3难度：0.7
解析
3．要使五边形木架（用五根木条钉成）不变形，至少要再钉上（　　）根木条．
A．1 B．2 C．3 D．4
组卷：931引用：20难度：0.9
解析
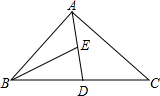4．已知AD是△ABC的中线，BE是△ABD的中线，若△ABC的面积为18，则△ABE的面积为（　　）
A．5 B．4.5 C．4 D．9
组卷：671引用：7难度：0.9
解析
5．下列命题是真命题的是（　　）
A．五边形的内角和是720°
B．三角形的任意两边之和大于第三边
C．三角形的外角大于任意一个内角
D．三角形的重心是这个三角形的三条角平分线的交点
组卷：31引用：1难度：0.5
解析
6．三角形的三个内角的度数之比为2：3：7，则这个三角形最大内角一定是（　　）
A．75° B．90° C．105° D．120°
组卷：908引用：10难度：0.8
解析
7．一个多边形的内角和为1800°，则这个多边形的边数为（　　）
A．9 B．10 C．11 D．12
组卷：1305引用：35难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8个小题，共75分）

22．【图形定义】
有一条高线相等的两个三角形称为等高三角形．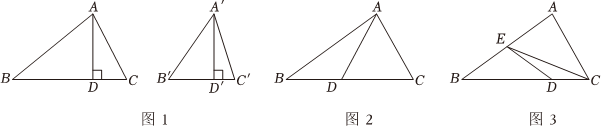

例如：如图1，在△ABC和△A′B′C′中，AD，A′D′分别是BC和B′C′边上的高线，且AD=A′D′，则△ABC和△A′B′C′是等高三角形．
【性质探究】
如图1，用S_△ABC，S_{△A′B′C′}分别表示△ABC和△A′B′C′的面积．
则
S
△
ABC
=
1
2
BC
⋅
AD
，
S
△
A
′
B
′
C
′
=
1
2
B
′
C
′
⋅
A
′
D
′
．
∵AD=A′D′，
∴S_△ABC：S_{△A′B′C′}=BC：B′C′．
【性质应用】
（1）如图2，D是△ABC的边BC上的一点．若BD=3，DC=4，则S_△ABD：S_△ADC=
．
（2）如图3，在△ABC中，D，E分别是BC和AB边上的点．若BE：AB=1：2，CD：BC=1：3，S_△ABC=1，则S_△BEC=
，S_△CDE=
．
【提示】∵△BEC和△ABC是等高三角形，∴S_△BEC：S_△ABC=BE：AB=1：2．∴
S
△
BEC
=
1
2
S
△
ABC
=
1
2
×
1
=
1
2
．∵△CDE和△BEC是等高三角形，∴S_△CDE：S_△BEC=CD：BC=1：3．∴
S
△
CDE
=
1
3
S
△
BEC
=
1
3
×
1
2
=
1
6
．
（3）如图3，在△ABC中，D，E分别是BC和AB边上的点，若BE：AB=1：m,CD：BC=1：n,S_△ABC=a,则S_△CDE=
．
【提示】∵△BEC和△ABC是等高三角形，∴S_△BEC：S_△ABC=BE：AB=1：m.∴
S
△
BEC
=
1
m
S
△
ABC
=
1
m
×
a
=
a
m
．∵△CDE和△BEC是等高三角形，∴S_△CDE：S_△BEC=CD：BC=1：n.∴
S
△
CDE
=
1
n
S
△
BEC
=
1
n
×
a
m
=
a
mn
．
组卷：45引用：1难度：0.5
解析
23．（1）问题发现：由“三角形的一个外角等于与它不相邻的两个内角的和”联想到四边形的外角．
如图①，∠1，∠2是四边形ABCD的两个外角．
∵四边形ABCD的内角和是360°，
∴∠A+∠D+（∠3+∠4）=360°，
又∵∠1+∠3+∠2+∠4=360°，
由此可得∠1，∠2与∠A，∠D的数量关系是
；
（2）知识应用：如图②，已知四边形ABCD，AE，DE分别是其外角∠NAD和∠MDA的平分线，若∠B+∠C=230°，求∠E的度数；
（3）拓展提升：如图③，四边形ABCD中，∠A=∠C=90°，∠CDN和∠CBM是它的两个外角，且∠CDP=
1
4
∠CDN，∠CBP=
1
4
∠CBM，求∠P的度数．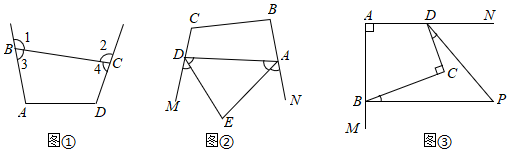
组卷：904引用：10难度：0.7
解析