（1）问题发现：由“三角形的一个外角等于与它不相邻的两个内角的和”联想到四边形的外角．
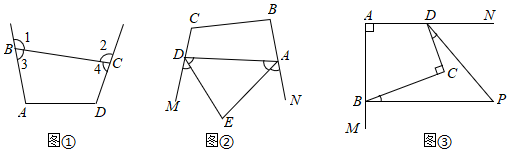
如图①，∠1，∠2是四边形ABCD的两个外角．
∵四边形ABCD的内角和是360°，
∴∠A+∠D+（∠3+∠4）=360°，
又∵∠1+∠3+∠2+∠4=360°，
由此可得∠1，∠2与∠A，∠D的数量关系是 ∠1+∠2=∠A+∠D∠1+∠2=∠A+∠D；
（2）知识应用：如图②，已知四边形ABCD，AE，DE分别是其外角∠NAD和∠MDA的平分线，若∠B+∠C=230°，求∠E的度数；
（3）拓展提升：如图③，四边形ABCD中，∠A=∠C=90°，∠CDN和∠CBM是它的两个外角，且∠CDP=14∠CDN，∠CBP=14∠CBM，求∠P的度数．
1
4
1
4
【答案】∠1+∠2=∠A+∠D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/21 8:0:9组卷：943引用：10难度：0.7
相似题
-
1．若十二边形的每一个内角都相等，那么它的内角的度数是 ．
发布：2025/6/16 22:0:2组卷：181引用：4难度：0.8 -
2．如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题．
（1）将如表的表格补充完整：
（2）根据规律，是否存在一个正n边形，使其中的∠α=20°？若存在，求出n的值；若不存在，请说明理由．正多边形的边数 3 4 5 6 …… n ∠α的度数 …… 发布：2025/6/16 22:30:4组卷：79引用：5难度：0.5 -
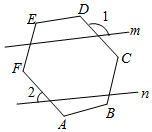3．如图，六边形ABCDEF的各角都相等，若m∥n,则∠1+∠2=°．发布：2025/6/16 21:30:2组卷：836引用：6难度：0.7
