2022-2023学年四川省成都市锦江区嘉祥外国语高级中学高一(下)月考数学试卷(6月份)
发布:2024/8/11 1:0:1
一、选择题(本题共8小题,每小题5分,共40分.每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.复数z=ai+b(a,b∈R)是纯虚数的充分不必要条件是( )
组卷:173引用:6难度:0.7 -
2.已知第二象限角α的终边与单位圆交于
,则sin2α=( )P(m,35)组卷:106引用:5难度:0.7 -
3.已知菱形ABCD边长为1,∠BAD=60°,则
=( )BD•DC组卷:185引用:2难度:0.8 -
4.已知直线l及三个互不重合的平面α,β,γ,下列结论错误的是( )
组卷:106引用:4难度:0.7 -
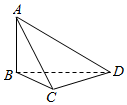 5.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )组卷:560引用:20难度:0.7
5.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )组卷:560引用:20难度:0.7 -
6.欧拉公式eix=cosx+isinx(其中e是自然对数的底,i为虚数单位)是由著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了指数函数与三角函数的关系,被誉为“数学中的天桥”.根据欧拉公式,若将
所表示的复数记为z,则e2π3i=( )z组卷:26引用:3难度:0.8 -
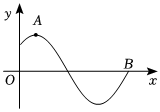 7.已知函数的部分图象如下所示,其中f(x)=2cos(ωx+φ)(ω>0,|φ|<π2),为了得到g(x)=2sin2x的图象,需将( )A(π12,2),B(7π12,0)组卷:266引用:5难度:0.8
7.已知函数的部分图象如下所示,其中f(x)=2cos(ωx+φ)(ω>0,|φ|<π2),为了得到g(x)=2sin2x的图象,需将( )A(π12,2),B(7π12,0)组卷:266引用:5难度:0.8
四、解答题(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
-
21.在直角梯形ABCD中,AD∥BC,
,∠ABC=90°(如图1).把△ABD沿BD翻折,使得二面角A-BD-C的平面角为θ(如图2),M、N分别是BD和BC中点.BC=2AD=2AB=22
(1)若E是线段BN的中点,动点F在三棱锥A-BMN表面上运动,并且总保持FE⊥BD,求动点F的轨迹的长度(可用θ表示),详细说明理由;
(2)若P、Q分别为线段AB与DN上一点,使得,令PQ与BD和AN所成的角分别为θ1和θ2,求sinθ1+sinθ2的取值范围.APPB=NQQD=λ(λ∈R)组卷:109引用:4难度:0.4 -
 22.如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,
22.如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,
∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
(Ⅰ)证明:EF⊥BC;
(Ⅱ)求直线EF与平面A1BC所成角的余弦值.
(Ⅲ)求二面角A-A1C-B的正弦值.组卷:1334引用:7难度:0.5


