2022-2023学年上海交大附中高一（下）期末数学试卷

一、填空题（本大题共12题，1-6题每题4分，7-12题每题5分，满分54分）

• 1．在平面直角坐标系中，过点（0，1）且倾斜角为45°的直线不经过第

  象限．
  组卷：178引用：1难度：0.7

  解析

• 2．已知向量

  a

  =

  （

  x

  ,

  1

  ）

  ，

  b

  =

  （

  -

  2

  ，

  3

  ）

  ，若

  a

  ⊥

  b

  ，则实数x=

  ．
  组卷：116引用：4难度：0.8

  解析

• 3．经过点（1，1）且在x轴和y轴上截距都相等的直线方程为

  ．
  组卷：369引用：2难度：0.7

  解析

• 4．已知数列{a_n}的前n项和S_n=-2n²+3n+1，则a_n=

  ．
  组卷：219引用：5难度：0.7

  解析

• 5．已知△ABC中，角A，B，C所对的边a=4，b=5，c=6，则sinA=

  ．
  组卷：1795引用：2难度：0.7

  解析

• 6．欧拉公式e^ix=cosx+isinx（i为虚数单位）是由瑞士著名数学家欧拉提出的，它将指数函数的定义域扩大到复数集，则复数

  2

  i

  e

  π

  4

  i

  的虚部为

  ．
  组卷：30引用：1难度：0.7

  解析

• 7．已知|z|=1，则|z+3-4i|的最大值是

  ．
  组卷：66引用：1难度：0.8

  解析

三、解答题（本大题共5题，满分76分，14'+14'+14'+16'+18'=76'）

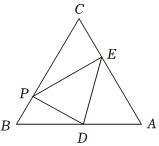• 20．已知△ABC中，a,b,c是角A，B，C所对的边，

  asin

  A

  +

  C

  2

  =

  bsin

  A

  ，且a=1．
  （1）求角B；
  （2）若AC=BC，在△ABC的边AB，AC上分别取D，E两点，使ADE沿线段DE折叠到平面BCE后，顶点A正好落在边BC（设为点P）上，设BP=x,AD=m,试求m关于x的函数解析式；
  （3）在（2）的条件下，求AD的最小值并求此时x的值．
  组卷：72引用：1难度：0.5

  解析

• 21．已知数列{a_n}，若{a_n+a_n+1}为等比数列，则称{a_n}具有性质P．
  （1）若数列{a_n}具有性质P，且a₁=a₂=1，a₃=3，求a₄、a₅的值；
  （2）若b_n=2ⁿ+（-1）ⁿ，判断数列{b_n}是否具有性质P并证明；
  （3）设c₁+c₂+⋯+c_n=n²+n,数列{d_n}具有性质P，其d₁=1，d₃-d₂=c₁，d₂+d₃=c₂，试求数列{d_n}的通项公式．
  组卷：119引用：7难度：0.5

  解析