2022-2023学年四川省泸州市泸县五中高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={-1，0，1，2}，B={x|x²≤1}，则A∩B=（　　）

  A．{-1，0，1}

  B．{0，1}

  C．{-1，1}

  D．{0，1，2}
  组卷：257引用：19难度：0.9

  解析

• 2．已知复数z满足

  z

  1

  -

  i

  =1+2i（其中i为虚数单位），则|z|=（　　）

  A．3

  B．2 2

  C．2

  D． 10
  组卷：203引用：5难度：0.8

  解析

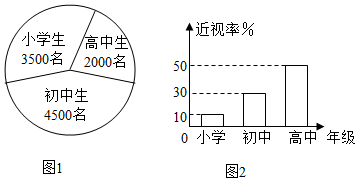• 3．已知某地区中小学生人数和近视情况分别如图1和图2所示．为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为（　　）

  A．200，20

  B．100，20

  C．200，10

  D．100，10
  组卷：1483引用：47难度：0.9

  解析

• 4．某学校在校学生有3000人，为了增强学生的体质，学校举行了跑步和登山比赛，每人都参加且只参加其中一项比赛，高一、高二、高三年级参加跑步的人数分别为a,b,c,且a：b：c=2：3：4，全校参加登山的人数占总人数的

  2

  5

  ．为了了解学生对本次比赛的满意程度，按分层抽样的方法从中抽取一个容量为300的样本进行调查，则应从高二年级参加跑步的学生中抽取（　　）

  A．15人

  B．30人

  C．45人

  D．60人
  组卷：165引用：6难度：0.8

  解析

• 5．O为▱ABCD两条对角线的交点，

  AB

  =4

  e

  1

  ，

  BC

  =6

  e

  2

  ，则

  DO

  =（　　）

  A．2 e 1 + e 2

  B．2 e 1 - e 2

  C．2 e 1 +3 e 2

  D．2 e 1 -3 e 2
  组卷：83引用：6难度：0.8

  解析

• 6．已知α，β，γ是三个不同的平面，m,n是两条不同的直线，则下列命题中正确的是（　　）

  A．若α⊥γ，β⊥γ，则α∥β	B．若m∥α，m∥β，则α∥β
  C．若m⊥α，n⊥α，则m∥n	D．若m∥α，n∥α，则m∥n
  组卷：73引用：8难度：0.6

  解析

• 7．已知在△ABC中，AB=3，AC=4，BC=

  10

  ，则

  AB

  •

  BC

  =（　　）

  A． - 3 4

  B． - 3 2

  C． 3 2

  D． 3 4
  组卷：194引用：9难度：0.8

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．如图，四棱锥P-ABCD的底面是正方形，PA⊥平面ABCD，PA=AB．点E是PD的中点，作EF⊥PC，交PC于点F．
  （1）设平面PAB与平面ACE的交线为l,试判断直线PB与直线l的位置关系，并给出证明；
  （2）求平面PAB与平面ACE所成的较小的二面角的余弦值；
  （3）求直线PD与平面AEF所成角的正切值．
  组卷：266引用：3难度：0.5

  解析

• 22．如图，设△ABC中角A，B，C所对的边分别为a,b,c,AD为BC边上的中线，已知c=1且2csinAcosB=asinA-bsinB+

  1

  4

  bsinC，cos∠BAD=

  21

  7

  ．
  （Ⅰ）求中线AD的长度；
  （Ⅱ）设点E、F分别为边AB，AC上的动点，线段EF交AD于G，且△AEF的面积为△ABC面积的一半，求

  AG

  •

  EF

  的最大值．
  组卷：167引用：4难度：0.3

  解析