当前位置：试卷中心 > 试卷详情

2022-2023学年北京市东城区东直门中学高二（上）期中数学试卷

发布：2024/7/14 8:0:9

1．已知数列{a_n}中，a_n+1=3a_n，a₁=2，则a₄等于（　　）
A．18 B．54 C．36 D．72
组卷：414引用：7难度：0.7
解析
2．甲、乙两人下棋，和棋的概率为50%．甲不输的概率为90%，则乙不输的概率为（　　）
A．60% B．50% C．40% D．30%
组卷：757引用：6难度：0.8
解析
3．已知空间向量
a
=（1，-1，0），
b
=（3，-2，1），则|
a
+
b
|=（　　）
A．
5
B．
6
C．5 D．
26
组卷：758引用：9难度：0.8
解析
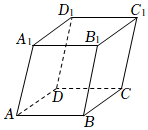4．如图，在平行六面体ABCD-A₁B₁C₁D₁中，
AB
+
AD
-
CC
1
=（　　）
A．
A
C
1
B．
A
1
C
C．
D
1
B
D．
D
B
1
组卷：414引用：24难度：0.7
解析
5．在公差不为零的等差数列{a_n}中，a₁=1，a₅是a₂，a₁₄的等比中项，则数列{a_n}前7项和S₇=（　　）
A．13 B．49 C．2⁶ D．2⁷-1
组卷：229引用：2难度：0.9
解析
6．已知向量
a
=
（
x
,
2
，
4
）
，
b
=
（
3
，
y
,-
2
）
，
c
=
（
1
，-
1
，
0
）
，若
（
a
+
c
）
∥
b
，则x+y=（　　）
A．-1 B．-3 C．
-
15
2
D．-8
组卷：83引用：2难度：0.7
解析
7．已知
a
n
=
1
n
2
+
n
，设数列{a_n}的前n项和为S_n，则S₂₀₂₂的值为（　　）
A．
2022
2021
B．
2020
2021
C．
2023
2022
D．
2022
2023
组卷：15引用：2难度：0.7
解析

21．某单位规定每位员工每年至少参加两项专业技能测试，测试通过可获得相应学分，每年获得的总学分不低于10分，该年度考核为合格．该单位员工甲今年可参加的专业技能测试有A、B、C、D四项，已知这四项专业技能测试的学分及员工甲通过各项专业技能测试的概率如表所示，且员工甲各项专业技能测试是否通过相互独立．

培训项目 A B C D

学分 5分 6分 4分 8分

员工甲通过测试的概率
4
5

3
4

5
6

1
2

（1）若员工甲参加A、B、C三项测试，求他本年度考核合格的概率：
（2）员工甲欲从A、B，C、D中选择三项参加测试，若要使他本年度考核合格的概率不低于
3
4
，应如何选择？请求出所有满足条件的方案．

组卷：165引用：3难度：0.8