当前位置：试卷中心 > 试卷详情

2022-2023学年北京市东城区东直门中学高一（下）期中数学试卷

发布：2024/5/10 8:0:9

一．选择题：（本题有12道小题，每小题4分，共48分）

1．在平面直角坐标系xOy中，若角α以x轴非负半轴为始边，其终边与单位圆交点的横坐标为
3
2
，则α的一个可能取值为（　　）
A．-60° B．-30° C．45° D．60°
组卷：473引用：5难度：0.8
解析
2．下列命题正确的是（　　）
A．单位向量都相等
B．模为0的向量与任意向量共线
C．平行向量不一定是共线向量
D．任一向量与它的相反向量不相等
组卷：704引用：7难度：0.9
解析
3．已知角α的终边在第三象限，且tanα=2，则sinα-cosα=（　　）
A．-1 B．1 C．-
5
5
D．
5
5
组卷：738引用：11难度：0.8
解析
4．已知P为△ABC所在平面内一点，
BC
=
2
CP
，则（　　）
A．
AP
=
-
1
2
AB
+
3
2
AC
B．
AP
=
1
3
AB
+
2
3
AC
C．
AP
=
3
2
AB
-
1
2
AC
D．
AP
=
2
3
AB
+
1
3
AC
组卷：968引用：8难度：0.7
解析
5．已知向量
a
=（2，4），
b
=（-1，1），则2
a
-
b
=（　　）
A．（5，7） B．（5，9） C．（3，7） D．（3，9）
组卷：3981引用：69难度：0.9
解析
6．已知点A（1，3），B（4，-1），则与向量
AB
同方向的单位向量为（　　）
A．
（
3
5
，-
4
5
）
B．
（
4
5
，-
3
5
）
C．
（
-
3
5
，
4
5
）
D．
（
-
4
5
，
3
5
）
组卷：4804引用：93难度：0.9
解析
7．向量
a
，
b
，
c
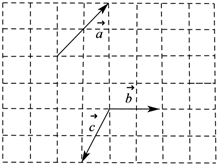在边长为1的正方形网格中的位置如图所示，则
（
a
-
b
）
•
c
=（　　）
A．-4 B．4 C．2 D．-8
组卷：655引用：7难度：0.7
解析
8．设点A，B，C不共线，则“
AB
与
AC
的夹角为锐角”是“|
AB
+
AC
|＞|
BC
|”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：4027引用：30难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题：（本题有6小题，共70分）

25．在△ABC中，内角A，B，C所对的边分别为a,b,c,向量
m
=
（
b
,
3
a
）
，向量
n
=
（
sin
B
，
sin
2
A
）
，且
m
∥
n
．
（Ⅰ）求∠A；
（Ⅱ）若△ABC的面积为
3
3
，再从条件①、条件②、条件③这三个条件中选择一个作为已知，使△ABC存在且唯一确定，求a的值．
条件①：
sin
C
=
2
7
7
；条件②：
b
c
=
3
3
4
；条件③：
cos
C
=
21
7
．
注：如果选择的条件不符合要求，第（Ⅱ）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．
组卷：147引用：1难度：0.6
解析
26．设正整数n≥3，集合A={a|a=（x₁，x₂，…，x_n），x_k∈R，k=1，2，…，n}，对应集合A中的任意元素a=（x₁，x₂，...x_n）和b=（y₁，y₂，...y_n），及实数λ，定义：当且仅当x_k=y_k（k=1，2，…，n）时a=b；a+b=（x₁+y₁，x₂+y₂，...x_n+y_n）；λa=（λx₁，λx₂，...λx_n）．若A的子集B={a₁，a₂，a₃}满足：当且仅当λ₁=λ₂=λ₃=0时，λ₁a₁+λ₂a₂+λ₃a₃=（0，0，…，0），则称B为A的完美子集．
（Ⅰ）当n=3时，已知集合B₁={（1，0，0），（0，1，0），（0，0，1）}，B₂={（1，2，3），（2，3，4），（4，5，6）}，分别判断这两个集合是否为A的完美子集，并说明理由；
（Ⅱ）当n=3时，已知集合B={（2m,m,m-1），（m,2m,m-1），（m,m-1，2m）}．若B不是A的完美子集，求m的值；
（Ⅲ）已知集合B={a₁，a₂，a₃}⊆A，其中a_i=（x_i1，x_i2，...x_in）（i=1，2，3）．若2|x_ii|＞|x_1i|+|x_2i|+|x_3i|对任意i=1，2，3都成立，判断B是否一定为A的完美子集．若是，请说明理由；若不是，请给出反例．
组卷：353引用：15难度：0.3
解析