2022-2023学年福建省福州市文博中学高一(下)期末数学试卷
发布:2024/7/7 8:0:9
一、单选题。(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1.若复数z满足(1-i)z=|1+i|,则z的虚部是( )
组卷:248引用:7难度:0.9 -
2.若|
|=a,|2|=2且(b-a)⊥b,则a与a的夹角是( )b组卷:756引用:53难度:0.9 -
3.某校从高一新生中随机抽取了一个容量为10的身高样本,数据(单位:cm)从小到大排序下:158,165,165,167,168,169,x,172,173,175.若样本数据的第60百分位数是170,则x=( )
组卷:237引用:5难度:0.8 -
4.正方形ABCD的边长是2,E是AB的中点,则
•EC=( )ED组卷:189引用:13难度:0.7 -
5.△ABC中,AC=
,BC=2,A=60°,则cosB=( )3组卷:443引用:4难度:0.7 -
6.为了解甲、乙两个班级学生的物理学习情况,从两个班学生的物理成绩(均为整数)中各随机抽查20个,得到如图所示的数据图(用频率分布直方图估计总体平均数时,每个区间的值均取该区间的中点值),关于甲、乙两个班级的物理成绩,下列结论正确的是( )
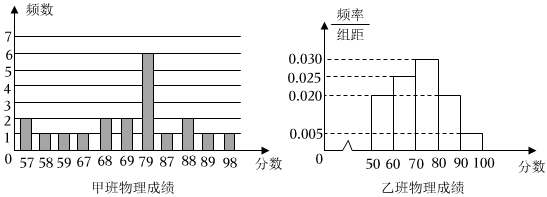 组卷:795引用:7难度:0.5
组卷:795引用:7难度:0.5 -
 7.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.有下列四个结论:
7.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.有下列四个结论:
①;φ=π3
②f(x)在上单调递增;[-7π12,-π12]
③f(x)的最小正周期T=π;
④f(x)的图象的一条对称轴为.x=π3
其中正确的结论有( )组卷:178引用:7难度:0.7
四、解答题。(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
 21.如图,在三棱锥A-BCD中,AB=AC=AD,底面是以BD为斜边的直角三角形,点M是BD的中点,点N在棱AD上.
21.如图,在三棱锥A-BCD中,AB=AC=AD,底面是以BD为斜边的直角三角形,点M是BD的中点,点N在棱AD上.
(1)证明:AM⊥平面BCD;
(2)若AB=BD=2BC,直线BN与平面BCD所成角的正切值为,求二面角N-BC-D的大小.32组卷:154引用:2难度:0.6 -
 22.如图,设△ABC中的角A,B,C所对的边是a,b,c,AD为∠BAC的角平分线,已知AB=1,,AD=34AB+14AC,点E,F分别为边AB,AC上的动点,线段EF交AD于点G,且△AEF的面积是△ABC面积的一半.AB|AB|•AC|AC|=12
22.如图,设△ABC中的角A,B,C所对的边是a,b,c,AD为∠BAC的角平分线,已知AB=1,,AD=34AB+14AC,点E,F分别为边AB,AC上的动点,线段EF交AD于点G,且△AEF的面积是△ABC面积的一半.AB|AB|•AC|AC|=12
(1)求边BC的长度;
(2)当时,求△AGF的面积.AG•EF=4528组卷:309引用:4难度:0.7


