当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省本溪十二中九年级（上）第二次月考数学试卷

发布：2024/8/17 2:0:1

一、选择题：（每题3分，共10小题，合计30分）

1．|-2022|的值（　　）
A．
1
2022
B．2022 C．
-
1
2022
D．-2022
组卷：402引用：14难度：0.9
解析
2．以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：1400引用：34难度：0.8
解析
3．下列计算正确的是（　　）
A．x²•x³=x⁶ B．（x-2）²=x²-4
C．（-3ab²）²=9a²b⁴ D．3a²-a²=3
组卷：396引用：10难度：0.7
解析
4．我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法．如图所示的几何体是可以形成“牟合方盖”的一种模型，它的俯视图是（　　）
A． B． C． D．
组卷：148引用：6难度：0.8
解析
5．已知△ABC∽△A′B′C′，AD和A′D′是它们的对应高线，若AD=5，A′D′=3，则△ABC与A'B'C′的面积比是（　　）
A．25：9 B．9：25 C．5：3 D．3：5
组卷：176引用：2难度：0.5
解析
6．为了保护环境加强环保教育，某中学组织学生参加义务收集废旧电池的活动，下面是随机抽取40名学生对收集废旧电池的数量进行的统计：

废旧电池数/节 4 5 6 7 8

人数/人 9 11 11 5 4

请根据学生收集到的废旧电池数，判断下列说法正确的是（　　）
A．样本为40名学生 B．众数是11节
C．中位数是6节 D．平均数是5.6节
组卷：943引用：16难度：0.7
解析
7．如图，直线y=kx+b（k≠0）与直线y=2x-1相交于点P（2，3）．根据图象可知，关于x的不等式kx+b＞2x-1的解集是（　　）
A．x＞2 B．x＜2 C．x＞3 D．x＜3
组卷：320引用：4难度：0.8
解析
8．如图，平行四边形ABCD，对角线AC、BD交于点O，EO⊥BD于O交BC于E，若△DEC的周长为8，则平行四边形ABCD的周长为（　　）
A．14 B．16 C．17 D．18
组卷：17引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（共8小题，19题10分，20～25题每题12分，26题14分，合计96分）

25．如图，△ABC是等腰直角三角形，且∠ACB=90°，AC=BC，直线MN经过点B，且MN∥AC，点P是斜边AB上一点，点D是直线MN上的一点，连接PD，将射线PD绕点P顺时针旋转90°得射线PE，射线PE交直线BC于点E．

（1）如图1，当点D在射线BN上，且点P为AB的中点时，请猜想线段PD与PE的数量关系，并加以证明；
（2）如图2，当点D在射线BN上，且点P不是AB的中点时，试判断三条线段BP，BD和BE的数量关系，并说明理由；
（3）点D在运动过程中，当∠PEB=30°，且PB=2时，请直接写出线段BD的长．
组卷：32引用：2难度：0.2
解析
26．已知抛物线y=ax²+bx+3的图象与x轴相交于点A和点B（1，0），与y轴交于点C，连接AC，有一动点D在线段AC上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F，AB=4，设点D的横坐标为m.

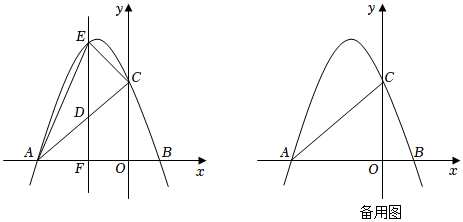
（1）求抛物线的解析式；
（2）连接AE、CE，当四边形AOCE的面积最大时，求点D的坐标及最大面积；
（3）D点在运动过程中，是否存在三角形DCE为等腰三角形，若存在，直接写出m值，若不存在，说明理由．
组卷：81引用：2难度：0.5
解析