2022-2023学年甘肃省白银市靖远四中高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．复数

  z

  =

  -

  2

  i

  （

  -

  1

  +

  3

  i

  ）

  的虚部为（　　）

  A．-2

  B．2

  C．2i

  D． 2 3
  组卷：24引用：4难度：0.8

  解析

• 2．设全集U=R，集合A={x|x＜0}，B={x|（x+1）（x-2）＞0}，则∁_U（A∪B）=（　　）

  A．（-∞，2]

  B．[0，+∞）

  C．[-1，2]

  D．[0，2]
  组卷：70引用：3难度：0.7

  解析

• 3．设向量

  e

  1

  ，

  e

  2

  ，

  e

  3

  不共面，已知

  AB

  =

  e

  1

  +

  e

  2

  +

  e

  3

  ，

  BC

  =

  e

  1

  +λ

  e

  2

  +

  e

  3

  ，

  CD

  =4

  e

  1

  +8

  e

  2

  +4

  e

  3

  ，若A，C，D三点共线，则λ=（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：425引用：6难度：0.8

  解析

• 4．已知数列0，lg3，lg5，lg7，…，根据该数列的规律，该数列中小于2的项有（　　）

  A．50项

  B．51项

  C．100项

  D．101项
  组卷：0引用：2难度：0.8

  解析

• 5．已知圆C：x²+y²-6x+4y-4=0，则过点M（4，-1）的最短弦所在直线l的方程为（　　）

  A．x+2y-2=0

  B．x-y-5=0

  C．x+y-3=0

  D．x-2y-6=0
  组卷：317引用：2难度：0.7

  解析

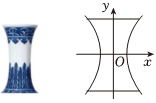• 6．如图，这是一个落地青花瓷，其外形被称为单叶双曲面，可以看成是双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  的一部分绕其虚轴所在直线旋转所形成的曲面．若该花瓶横截面圆的最小直径为8cm,瓶高等于双曲线C的虚轴长，则该花瓶的瓶口直径为（　　）

  A． 16 2 cm

  B．24cm

  C．32cm

  D． 8 2 cm
  组卷：167引用：8难度：0.5

  解析

• 7．将函数f（x）=sin（ωx+1）（ω＞0）的图象向右平移1个单位长度后，得到的图象关于原点对称，则ω的最小值为（　　）

  A． 1 2

  B．1

  C．2

  D．4
  组卷：80引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  3

  2

  ，左、右焦点分别为F₁，F₂，左、上顶点分别为A₁，B₁，且△A₁B₁F₁外接圆的半径为

  10

  ，O为坐标原点．
  （1）求椭圆C的标准方程；
  （2）设A（m,1）（m＞0）为椭圆C上一点，直线OA的平行线l与椭圆C相交于M，N两点，直线AM，AN分别与y轴交于P，Q两点，求线段PQ的中点的纵坐标．
  组卷：24引用：1难度：0.5

  解析

• 22．某同学正在研究投掷骰子的概率问题，在连续3次得到6点朝上的结果时，他产生了一个疑问：在连续多少次6点朝上时，是否该合理怀疑骰子不是均匀的？带着这个疑问，他研究了以下问题：有两个骰子，一个是正常的、均匀的1号骰子，另一个是不均匀的2号骰子．经测1试，投掷2号骰子得到6点朝上的概率为

  1

  2

  ．
  （1）若等可能地选择其中一个骰子，连续投掷3次，在得到都是6点朝上的结果的前提下，求这个骰子是2号骰子的概率．
  （2）若每次都等可能地选择其中一个骰子，投掷了10次，在得到都是6点朝上的结果的前提下，设这10次中有X次用了2号骰子的概率为P（X），试问当X取何值时P（X）最大？并求P（X）的最大值．
  组卷：91引用：1难度：0.6

  解析