当前位置：试卷中心 > 试卷详情

2023-2024学年北京161中高二（上）段考数学试卷

发布：2024/9/17 10:0:12

一、选择题：本大题共12道小题，每小题4分，共48分。在每小题给出的四个选项中，只有一项符合题目的要求。把正确答案涂写在答题卡上相应的位置。

1．已知点A（2，1，0）和点B（0，-3，4），则向量
AB
=（　　）
A．（-2，-4，4） B．（2，4，-4） C．（-2，-2，4） D．（2，2，-4）
组卷：46引用：5难度：0.7
解析
2．设
i
，
j
，
k
是两两不共线的向量，且向量
a
=
-
i
+
2
j
+
4
k
，
b
=
3
i
-
2
j
-
k
，则
2
a
-
3
b
=（　　）
A．
11
i
-
2
j
+
5
k
B．
-
11
i
-
2
j
+
5
k
C．
-
11
i
+
10
j
+
11
k
D．
11
i
-
10
j
-
11
k
组卷：31引用：3难度：0.7
解析
3．点M（3，-2，1）关于平面yOz对称的点的坐标是（　　）
A．（-3，-2，1 ） B．（-3，2，-1） C．（-3，-2，-1） D．（-3，2，1）
组卷：232引用：23难度：0.9
解析
4．已知
a
=
（
-
1
，
0
，-
1
）
，
b
=
（
1
，
1
，
2
）
，则向量
a
在
b
方向上的投影数量为（　　）
A．-3 B．
-
6
2
C．
-
3
2
2
D．
6
2
组卷：50引用：2难度：0.5
解析
5．与向量
AB
=
（
1
，-
1
，
2
）
共线的单位向量是（　　）
A．
（
1
2
，-
1
2
，
2
2
）
B．
（
1
2
，-
1
2
，
2
2
）
和
（
-
1
2
，
1
2
，-
2
2
）
C．
（
-
1
2
，
1
2
，-
2
2
）
D．
（
1
2
，
1
2
，
2
2
）
和
（
-
1
2
，-
1
2
，-
2
2
）
组卷：91引用：2难度：0.7
解析
6．已知向量
a
=
（
1
，
1
，
0
）
，
b
=
（
1
，-
1
，
0
）
，若
（
a
+
λ
b
）
⊥
（
a
+
μ
b
）
，则（　　）
A．λ+μ=1 B．λ+μ=-1 C．λμ=1 D．λμ=-1
组卷：59引用：2难度：0.7
解析
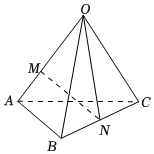7．如图，空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在OA上，OM=2MA，点N为BC中点，则
MN
等于（　　）
A．
1
2
a
-
2
3
b
+
1
2
c
B．-
2
3
a
+
1
2
b
+
1
2
c
C．
1
2
a
+
1
2
b
-
1
2
c
D．-
2
3
a
+
2
3
b
-
1
2
c
组卷：100引用：13难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：本大题共5小题，共72分。解答应写出必要的文字说明、证明过程或演算步骤。

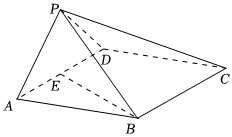22．如图，在四棱锥P-ABCD中，底面ABCD为菱形，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，
∠
BAD
=
π
3
，E是线段AD的中点，连结BE．
（Ⅰ）求证：BE⊥PA；
（Ⅱ）在线段PB上是否存在点F，使得EF∥平面PCD？若存在，求出
PF
PB
的值；若不存在，说明理由．
组卷：123引用：1难度：0.6
解析
23．已知集合X={x₁，x₂，⋯，x₈}是集合S={2007，2008，2009，⋯，2022，2023}的一个含有8个元素的子集．
（1）当X={2007，2008，2011，2013，2017，2019，2022，2023}时，设x_i，x_j∈X（1≤i,j≤8）：
（i）写出方程x_i-x_j=2的解（x_i，x_j）；
（ii）若方程x_i-x_j=k（k＞0）至少有三组不同的解，写出k的所有可能取值；
（2）证明：对任意一个X，存在正整数k,使得方程x_i-x_j=k（1≤i,j≤8）至少有三组不同的解．
组卷：5引用：2难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． 11 i - 2 j + 5 k	B． - 11 i - 2 j + 5 k
C． - 11 i + 10 j + 11 k	D． 11 i - 10 j - 11 k

A． 1 2 a - 2 3 b + 1 2 c	B．- 2 3 a + 1 2 b + 1 2 c
C． 1 2 a + 1 2 b - 1 2 c	D．- 2 3 a + 2 3 b - 1 2 c

2023-2024学年北京161中高二（上）段考数学试卷

一、选择题：本大题共12道小题，每小题4分，共48分。在每小题给出的四个选项中，只有一项符合题目的要求。把正确答案涂写在答题卡上相应的位置。

1．已知点A（2，1，0）和点B（0，-3，4），则向量AB=（ ）

2．设i，j，k是两两不共线的向量，且向量a=-i+2j+4k，b=3i-2j-k，则2a-3b=（ ）

3．点M（3，-2，1）关于平面yOz对称的点的坐标是（ ）

4．已知a=（-1，0，-1），b=（1，1，2），则向量a在b方向上的投影数量为（ ）

5．与向量AB=（1，-1，2）共线的单位向量是（ ）

6．已知向量a=（1，1，0），b=（1，-1，0），若（a+λb）⊥（a+μb），则（ ）

7．如图，空间四边形OABC中，OA=a，OB=b，OC=c，点M在OA上，OM=2MA，点N为BC中点，则MN等于（ ）

三、解答题：本大题共5小题，共72分。解答应写出必要的文字说明、证明过程或演算步骤。

1．已知点A（2，1，0）和点B（0，-3，4），则向量
AB
=（　　）

2．设
i
，
j
，
k
是两两不共线的向量，且向量
a
=
-
i
+
2
j
+
4
k
，
b
=
3
i
-
2
j
-
k
，则
2
a
-
3
b
=（　　）

3．点M（3，-2，1）关于平面yOz对称的点的坐标是（　　）

4．已知
a
=
（
-
1
，
0
，-
1
）
，
b
=
（
1
，
1
，
2
）
，则向量
a
在
b
方向上的投影数量为（　　）

5．与向量
AB
=
（
1
，-
1
，
2
）
共线的单位向量是（　　）

6．已知向量
a
=
（
1
，
1
，
0
）
，
b
=
（
1
，-
1
，
0
）
，若
（
a
+
λ
b
）
⊥
（
a
+
μ
b
）
，则（　　）

7．如图，空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在OA上，OM=2MA，点N为BC中点，则
MN
等于（　　）