2022-2023学年江西省抚州市高二（上）质检数学试卷

一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知直线l平分圆x²+（y-3）²=4，且与直线x+y=0垂直，则直线l的方程是（　　）

  A．x+y-2=0

  B．x-y+2=0

  C．x+y-3=0

  D．x-y+3=0
  组卷：62引用：3难度：0.8

  解析

• 2．三名学生分别从5门选修课中选修一门课程，不同的选法有（　　）

  A．125种

  B．243种

  C．60种

  D．10种
  组卷：591引用：6难度：0.8

  解析

• 3．古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．若椭圆C的中心为原点，焦点F₁，F₂均在x轴上，C的面积为

  2

  3

  π

  ，且短轴长为

  2

  3

  ，则C的标准方程为（　　）

  A． x 2 12 + y 2 = 1

  B． x 2 4 + y 2 3 = 1

  C． x 2 3 + y 2 4 = 1

  D． x 2 16 + y 2 3 = 1
  组卷：271引用：8难度：0.8

  解析

• 4．已知坐标平面内三点

  A

  （

  -

  1

  ，

  1

  ）

  ，

  B

  （

  1

  ，

  1

  ）

  ，

  C

  （

  2

  ，

  3

  +

  1

  ）

  ，D为△ABC的边AC上一动点，则直线BD斜率k的变化范围是（　　）

  A． [ 0 ， 3 3 ]	B． （ - ∞ ， 0 ] ∪ [ 3 3 ， + ∞ ）
  C． [ 3 3 ， 3 ]	D． （ - ∞ ， 0 ] ∪ [ 3 ， + ∞ ）
  组卷：180引用：2难度：0.5

  解析

• 5．已知圆x²+y²-6x=0，过点（1，2）的直线被该圆所截得的弦的长度的最小值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：7195引用：42难度：0.7

  解析

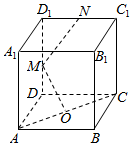• 6．在正方体ABCD-A₁B₁C₁D₁中，O是底面ABCD的中心，M、N分别是棱DD₁、D₁C₁的中点，则直线OM（　　）

  A．和AC、MN都垂直

  B．垂直于AC，但不垂直于MN

  C．垂直于MN，但不垂直于AC

  D．与AC、MN都不垂直
  组卷：387引用：12难度：0.9

  解析

• 7．如图，设F₁、F₂分别是椭圆的左、右焦点，点P是以F₁F₂为直径的圆与椭圆在第一象限内的一个交点，延长PF₂与椭圆交于点Q，若|PF₁|=4|QF₂|，则直线PF₂的斜率为（　　）

  A．-2

  B．-1

  C． - 1 2

  D．1
  组卷：623引用：11难度：0.6

  解析

四、解答题：本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．已知抛物线C：x²=2py（p＞0）上第一象限的一点P（x,1）到其焦点的距离为2．
  （1）求抛物线C的方程和P点坐标；
  （2）过点

  （

  -

  1

  ，

  1

  2

  ）

  的直线l交抛物线C于A、B，若∠APB的角平分线与y轴垂直，求弦AB的长．
  组卷：51引用：7难度：0.5

  解析

• 22．已知M是椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）上一点，F₁、F₂分别为椭圆C的左、右焦点，且|F₁F₂|=2，∠F₁MF₂=

  π

  3

  ，△F₁MF₂的面积为

  3

  ．
  （1）求椭圆C的方程；
  （2）直线l过椭圆C右焦点F₂，交该椭圆于A、B两点，AB中点为Q，射线OQ交椭圆于P，记△AOQ的面积为S₁，△BPQ的面积为S₂，若S₂=3S₁，求直线l的方程．
  组卷：104引用：2难度：0.4

  解析