2023-2024学年陕西省西安中学高二（上）第一次月考数学试卷

一、单项选择题：本题共8小题，每小题4分，共32分．在每小题给出的四个选项中，只有一项是符合题目要求．

• 1．设直线l方向向量

  v

  =

  （

  x

  ,

  1

  ，

  2

  ）

  ，平面α的法向量

  n

  =

  （

  -

  1

  ，

  1

  ，

  2

  ）

  ，若l⊥α，则x=（　　）

  A．-1

  B．0

  C．5

  D．4
  组卷：121引用：3难度：0.5

  解析

• 2．设点

  A

  （

  1

  ，-

  1

  ，

  2

  ）

  关于坐标原点的对称点是B，则|AB|等于（　　）

  A．4

  B． 2 3

  C． 2 2

  D．2
  组卷：109引用：6难度：0.8

  解析

• 3．已知向量

  a

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，则向量

  b

  在向量

  a

  上的投影向量为（　　）

  A．（0，-1，-1）

  B．（-1，0，-1）

  C． （ 0 ， 1 2 ， 1 2 ）

  D． （ 1 2 ， 0 ， 1 2 ）
  组卷：210引用：8难度：0.8

  解析

• 4．如果AB＞0且BC＜0，那么直线Ax+By+C=0不经过（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：433引用：12难度：0.8

  解析

• 5．如图，某圆锥SO的轴截面SAC是等边三角形，点B是底面圆周上的一点，且

  ∠

  AOB

  =

  2

  π

  3

  ，点M是SA的中点，则异面直线AB与CM所成角的余弦值是（　　）

  A． 3 4

  B． 7 4

  C． 1 3

  D． 3 2
  组卷：112引用：6难度：0.7

  解析

• 6．已知O为坐标原点，

  OA

  =（1，2，3），

  OB

  =（2，1，2），

  OP

  =（1，1，2），点Q在直线OP上运动，则当

  QA

  •

  QB

  取得最小值时，点Q的坐标为（　　）

  A． （ 1 2 ， 3 4 ， 1 3 ）

  B． （ 1 2 ， 2 3 ， 3 4 ）

  C． （ 4 3 ， 4 3 ， 8 3 ）

  D． （ 4 3 ， 4 3 ， 7 3 ）
  组卷：221引用：4难度：0.7

  解析

四、解答题：本小题共4小题，共48分，解答应写出文字说明、证明过程或演算步骤．

• 19．如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，AB⊥AC，AB=AC=AA₁=1，M为线段A₁C₁上一点．
  （1）求证：BM⊥AB₁；
  （2）若直线AB₁与平面BCM所成角为

  π

  4

  ，求点A₁到平面BCM的距离．
  组卷：151引用：12难度：0.5

  解析

• 20．如图1，四边形ABCD是平行四边形，AB=2AD=2，∠ADC=60°，E是CD的中点，将平行四边形ABCD沿着AE翻折，使平面ADE⊥平面ABCE（如图2），点G是△ADE的重心，连结AC，BE交于点F．
  
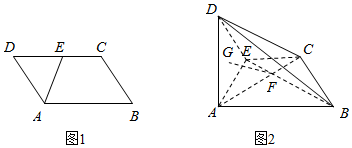
  （1）求证：GF∥平面CDE；
  （2）求直线GF与平面BCD所成角的正弦值．
  组卷：105引用：5难度：0.6

  解析