2023-2024学年湖南省株洲市炎陵县高二（上）入学数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题的四个选项中，只有一项是符合题目要求的．

• 1．若复数z满足（1+z）i=1-z（i为虚数单位），则z=（　　）

  A．-i

  B．i

  C．1-i

  D．1+i
  组卷：157引用：5难度：0.8

  解析

• 2．已知向量

  a

  =（1，2），

  b

  =（-2，t），若

  a

  ∥

  b

  ，则t=（　　）

  A．-4

  B．1

  C．2

  D．4
  组卷：855引用：17难度：0.8

  解析

• 3．已知圆锥轴截面为正三角形，母线长为4，则该圆锥的体积等于（　　）

  A． 8 3 3 π

  B． 8 3 π

  C． 16 3 π

  D．8π
  组卷：25引用：1难度：0.7

  解析

• 4．已知有样本数据2、4、5、6、8，则该样本的方差为（　　）

  A．5

  B．4

  C．2

  D．0
  组卷：59引用：3难度：0.9

  解析

• 5．已知两条不同直线l,m,两个不同平面α，β，则下列命题正确的是（　　）

  A．若α∥β，l⊂α，m⊂β，则l∥m	B．若α∥β，m∥α，l⊥β，则l⊥m
  C．若α⊥β，l⊥α，m⊥β，则l∥m	D．若α⊥β，l∥α，m∥β，则l⊥m
  组卷：590引用：10难度：0.6

  解析

• 6．如图是根据某市1月1日至1月10日的最低气温（单位：℃）的情况绘制的折线统计图，由图可知这10天的最低气温的第50百分位数是（　　）

  A．2℃

  B．1℃

  C．0℃

  D．-2℃
  组卷：100引用：6难度：0.8

  解析

• 7．棣莫弗公式（cosx+i•sinx）ⁿ=cos（nx）+i•sin（nx）（其中i为虚数单位）是由法国数学家棣莫弗（1667-1754）发现的，根据棣莫弗公式可知，复数

  （

  cos

  π

  3

  +

  i

  •

  sin

  π

  3

  ）

  4

  在复平面内所对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：101引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

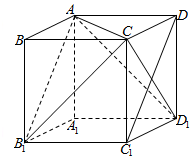• 21．已知直四棱柱ABCD-A₁B₁C₁D₁的所有棱长均为2，且∠A₁B₁C₁=60°．
  （Ⅰ）求证：C₁D∥平面AB₁C；
  （Ⅱ）求二面角B₁-AC-D₁的余弦值．
  组卷：296引用：3难度：0.5

  解析

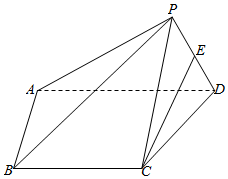• 22．如图，已知四棱锥P-ABCD，AD∥BC且AB⊥AD，

  AD

  =

  6

  2

  ，AB=4，

  BC

  =

  4

  2

  ，△PAD的面积等于

  12

  2

  ，E是PD是中点．
  （Ⅰ）求四棱锥P-ABCD体积的最大值；
  （Ⅱ）若

  PB

  =

  4

  5

  ，

  tan

  ∠

  PAD

  =

  2

  2

  ．
  （ⅰ）求证：AD⊥PC；
  （ⅱ）求直线CE与平面PBC所成角的正弦值．
  组卷：445引用：2难度：0.3

  解析