高中数学试卷真题_高中数学试卷分析

当前位置：章节挑题

请展开查看知识点列表

人教A版（2019）：必修第二册

教材版本: 人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）沪教版（2020）湘教版（2020）鄂教版（2019）人教A版人教B版北师大版苏教版沪教版湘教版大纲版

年级: 必修第一册必修第二册选择性必修第一册选择性必修第二册选择性必修第三册

第六章平面向量及其应用
第七章复数
第八章立体几何初步
第九章统计
第十章概率

更多>>

原创

更新中

【优学堂】2026年高考数学一轮复习

明确考点剖析考向配加典例和变式题真题演练及精选模拟全方位助力备考

浏览次数：4226 更新：2025年06月23日

原创

更新中

《黄金讲练》2025-2026学年人教A版（2019）必修第一册高一同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：765 更新：2025年06月23日

1191．下列选项中，P，Q，R，S分别是所在棱的中点，刚这四个点不共面的是（　　）
A． B． C． D．
发布：2024/5/23 20:38:36组卷：715引用：5难度：0.7
解析
1192．设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且面积为9
3
，则三棱锥D-ABC体积的最大值为（　　）
A．12
3
B．18
3
C．24
3
D．54
3
发布：2024/5/23 20:38:36组卷：9444引用：60难度：0.7
解析

1193．某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）．现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）．（1）A类工人中和B类工人各抽查多少工人？
（2）从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1：

生产能力分组 [100，110） [110，120） [120，130） [130，140） [140，150）

人数 4 8 x 5 3

表2：

生产能力分组 [110，120） [120，130） [130，140） [140，150）

人数 6 y 36 18

①先确定x,y,再在答题纸上完成下列频率分布直方图．就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）
②分别估计A类工人和B类工人生产能力的平均数，并估计该工厂工人和生产能力的平均数（同一组中的数据用该区间的中点值作代表）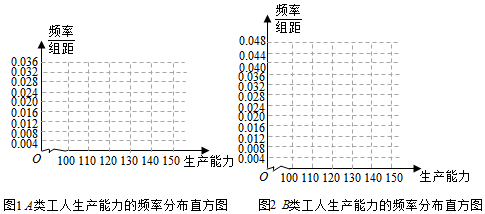

发布：2024/5/23 20:38:36组卷：250引用：6难度：0.3

解析

1194．设复数z=
1
2
+
3
2
i（i是虚数单位），则z+z²+…+z²⁰²⁰=
，z+2z²+3z³+4z⁴+5z⁵+6z⁶=
．
发布：2024/5/23 20:38:36组卷：23引用：2难度：0.6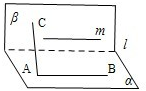
解析
1195．已知平面α⊥平面β，α∩β=l,点A∈α，A∉l,直线AB∥l,直线AC⊥l,直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（　　）
A．AB∥m B．AC⊥m C．AB∥β D．AC⊥β
发布：2024/5/23 20:38:36组卷：655引用：33难度：0.9
解析
1196．已知α、β是两个平面，a、l是两条直线，且α∩β=l,a∥α，a∥β．求证：a∥l.
发布：2024/5/23 20:38:36组卷：7引用：2难度：0.7
解析
1197．E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则AC与平面EFGH的位置关系是
．
发布：2024/5/23 20:38:36组卷：15引用：2难度：0.5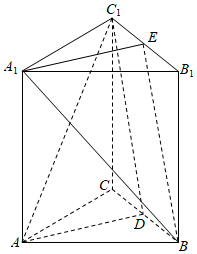
解析
1198．如图，在直三棱柱ABC-A₁B₁C₁中，点D，E分别是BC与B₁C₁的中点．
（1）求证：平面A₁EB∥平面ADC₁；
（2）若BC=AC=2，AD=
7
，CC₁=3，求三棱锥A-C₁CD的体积．
发布：2024/5/23 20:38:36组卷：233引用：3难度：0.5
解析
1199．在复平面内，O是原点，向量
OA
对应的复数是2+i.
（1）如果点A关于实轴的对称点为B，求向量
OB
对应的复数；
（2）如果（1）中点B关于虚轴的对称点为C，求点C对应的复数．
发布：2024/5/23 20:38:36组卷：132引用：3难度：0.5
解析
1200．甲、乙两人独立地破译某密码．他们能破译的概率分别为
1
3
和
1
4
．求：
（Ⅰ）两人都能破译的概率；
（Ⅱ）两人都不能破译的概率；
（Ⅲ）恰有一人能破译的概率；
（Ⅳ）至多有一人能破译的概率．
发布：2024/5/23 20:38:36组卷：28引用：1难度：0.5
解析

首页上一页 …117 118 119 120 …下一页尾页

生产能力分组	[100，110）	[110，120）	[120，130）	[130，140）	[140，150）
人数	4	8	x	5	3

1191．下列选项中，P，Q，R，S分别是所在棱的中点，刚这四个点不共面的是（ ）

1192．设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且面积为93，则三棱锥D-ABC体积的最大值为（ ）

1194．设复数z=12+32i（i是虚数单位），则z+z2+…+z2020=，z+2z2+3z3+4z4+5z5+6z6=．

1195．已知平面α⊥平面β，α∩β=l,点A∈α，A∉l,直线AB∥l,直线AC⊥l,直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（ ）

1196．已知α、β是两个平面，a、l是两条直线，且α∩β=l,a∥α，a∥β．求证：a∥l.

1197．E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则AC与平面EFGH的位置关系是 ．

1198．如图，在直三棱柱ABC-A1B1C1中，点D，E分别是BC与B1C1的中点．（1）求证：平面A1EB∥平面ADC1；（2）若BC=AC=2，AD=7，CC1=3，求三棱锥A-C1CD的体积．

1199．在复平面内，O是原点，向量OA对应的复数是2+i.（1）如果点A关于实轴的对称点为B，求向量OB对应的复数；（2）如果（1）中点B关于虚轴的对称点为C，求点C对应的复数．

1200．甲、乙两人独立地破译某密码．他们能破译的概率分别为13和14．求：（Ⅰ）两人都能破译的概率；（Ⅱ）两人都不能破译的概率；（Ⅲ）恰有一人能破译的概率；（Ⅳ）至多有一人能破译的概率．

1191．下列选项中，P，Q，R，S分别是所在棱的中点，刚这四个点不共面的是（　　）

1192．设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且面积为9
3
，则三棱锥D-ABC体积的最大值为（　　）

1194．设复数z=
1
2
+
3
2
i（i是虚数单位），则z+z²+…+z²⁰²⁰=
，z+2z²+3z³+4z⁴+5z⁵+6z⁶=
．

1195．已知平面α⊥平面β，α∩β=l,点A∈α，A∉l,直线AB∥l,直线AC⊥l,直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（　　）

1197．E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则AC与平面EFGH的位置关系是
．

1198．如图，在直三棱柱ABC-A₁B₁C₁中，点D，E分别是BC与B₁C₁的中点．
（1）求证：平面A₁EB∥平面ADC₁；
（2）若BC=AC=2，AD=
7
，CC₁=3，求三棱锥A-C₁CD的体积．

1199．在复平面内，O是原点，向量
OA
对应的复数是2+i.
（1）如果点A关于实轴的对称点为B，求向量
OB
对应的复数；
（2）如果（1）中点B关于虚轴的对称点为C，求点C对应的复数．

1200．甲、乙两人独立地破译某密码．他们能破译的概率分别为
1
3
和
1
4
．求：
（Ⅰ）两人都能破译的概率；
（Ⅱ）两人都不能破译的概率；
（Ⅲ）恰有一人能破译的概率；
（Ⅳ）至多有一人能破译的概率．