高中数学试卷真题_高中数学试卷分析

当前位置：章节挑题

请展开查看知识点列表

人教A版（2019）：必修第二册

教材版本: 人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）沪教版（2020）湘教版（2020）鄂教版（2019）人教A版人教B版北师大版苏教版沪教版湘教版大纲版

年级: 必修第一册必修第二册选择性必修第一册选择性必修第二册选择性必修第三册

第六章平面向量及其应用
第七章复数
第八章立体几何初步
第九章统计
第十章概率

更多>>

原创

更新中

【优学堂】2026年高考数学一轮复习

明确考点剖析考向配加典例和变式题真题演练及精选模拟全方位助力备考

浏览次数：2859 更新：2025年06月18日

原创

更新中

《黄金讲练》2025-2026学年人教A版（2019）选择性必修第一册高二同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：183 更新：2025年06月18日

2161．甲乙两运动员进行乒乓球比赛，采用7局4胜制．在一局比赛中，先得11分的运动员为胜方，但打到10平以后，先多得2分者为胜方．在10平后，双方实行轮换发球法，每人每次只发1个球．若在某局比赛中，甲发球赢球的概率为
1
2
，甲接发球赢球的概率为
2
5
，则在比分为10：10后甲先发球的情况下，甲以13：11赢下此局的概率为（　　）
A．
2
25
B．
3
10
C．
1
10
D．
3
25
发布：2024/4/20 14:35:0组卷：331引用：7难度：0.8
解析
2162．已知复数z=2+i（i是虚数单位）是关于x的实系数方程x²+px+q=0在复数范围内的一个根．
（1）求p+q的值；
（2）复数w满足z•w是实数，且|w|=2
5
，求复数w.
发布：2024/4/20 14:35:0组卷：115引用：4难度：0.6
解析
2163．在锐角△ABC中，角A，B，C所对的边分别为a,b,c.已知2bsinA-
3
a=0．
（Ⅰ）求角B的大小；
（Ⅱ）求cosA+cosB+cosC的取值范围．
发布：2024/4/20 14:35:0组卷：9283引用：24难度：0.6
解析
2164．如图，在矩形ABCD中，AB=
2
，BC=2，点E为BC的中点，点F在边CD上，若
AB
•
AF
=
2
，则
AE
•
BF
的值是
．
发布：2024/4/20 14:35:0组卷：3412引用：69难度：0.5
解析
2165．对于空间三条直线，有下列四个条件：
①三条直线两两相交且不共点：
②三条直线两两平行；
③三条直线共点；
④有两条直线平行，第三条直线和这两条直线都相交．
其中，使三条直线共面的充分条件有
．
发布：2024/4/20 14:35:0组卷：76引用：7难度：0.7
解析
2166．某公司为了解用户对其产品的满意度，从甲、乙两地区分别随机调查了100个用户，根据用户对产品的满意度评分，分别得到甲地区和乙地区用户满意度评分的频率分布直方图．

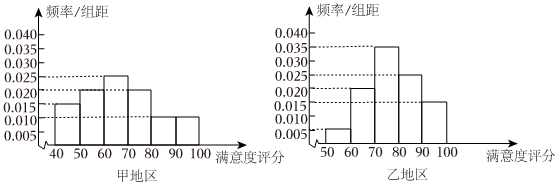
若甲地区和乙地区用户满意度评分的中位数分别为m₁，m₂；方差分别为
s
2
1
，
s
2
2
，则下面正确的是（　　）
A．
m
1
＞
m
2
，
s
2
1
＞
s
2
2
B．
m
1
＞
m
2
，
s
2
1
＜
s
2
2
C．
m
1
＜
m
2
，
s
2
1
＜
s
2
2
D．
m
1
＜
m
2
，
s
2
1
＞
s
2
2
发布：2024/4/20 14:35:0组卷：104引用：3难度：0.7
解析
2167．已知复数z满足
|
z
|
=
2
，z²的虚部为2．
（1）求复数z；
（2）设z、z²、z-z²在复平面上的对应点分别为A、B、C，求△ABC的面积．
发布：2024/4/20 14:35:0组卷：1537引用：14难度：0.3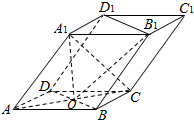
解析
2168．如图，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是正方形，O为底面中心，A₁O⊥平面ABCD，AB=AA₁=
2
．
（Ⅰ）证明：平面A₁BD∥平面CD₁B₁；
（Ⅱ）求三棱柱ABD-A₁B₁D₁的体积．
发布：2024/4/20 14:35:0组卷：3325引用：29难度：0.3
解析

2169．李明在10场篮球比赛中的投篮情况统计如下（假设各场比赛相互独立）；

场次投篮次数命中次数场次投篮次数命中次数

主场1 22 12 客场1 18 8

主场2 15 12 客场2 13 12

主场3 12 8 客场3 21 7

主场4 23 8 客场4 18 15

主场5 24 20 客场5 25 12

（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率；
（2）从上述比赛中随机选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一场不超过0.6的概率；
（3）记
x
是表中10个命中次数的平均数，从上述比赛中随机选择一场，记X为李明在这场比赛中的命中次数，比较EX与
x
的大小（只需写出结论）．

发布：2024/4/20 14:35:0组卷：1250引用：14难度：0.5

解析

2170．若
OA
=（-1，2），
OB
=（1，-1），则
AB
=（　　）
A．（-2，3） B．（0，1） C．（-1，2） D．（2，-3）
发布：2024/4/20 14:35:0组卷：1027引用：12难度：0.9
解析

首页上一页 …217 218 219 220 …下一页尾页

A． m 1 ＞ m 2 ， s 2 1 ＞ s 2 2	B． m 1 ＞ m 2 ， s 2 1 ＜ s 2 2
C． m 1 ＜ m 2 ， s 2 1 ＜ s 2 2	D． m 1 ＜ m 2 ， s 2 1 ＞ s 2 2

场次	投篮次数	命中次数	场次	投篮次数	命中次数
主场1	22	12	客场1	18	8
主场2	15	12	客场2	13	12
主场3	12	8	客场3	21	7
主场4	23	8	客场4	18	15
主场5	24	20	客场5	25	12

2162．已知复数z=2+i（i是虚数单位）是关于x的实系数方程x2+px+q=0在复数范围内的一个根．（1）求p+q的值；（2）复数w满足z•w是实数，且|w|=25，求复数w.

2163．在锐角△ABC中，角A，B，C所对的边分别为a,b,c.已知2bsinA-3a=0．（Ⅰ）求角B的大小；（Ⅱ）求cosA+cosB+cosC的取值范围．

2164．如图，在矩形ABCD中，AB=2，BC=2，点E为BC的中点，点F在边CD上，若AB•AF=2，则AE•BF的值是 ．

2165．对于空间三条直线，有下列四个条件：①三条直线两两相交且不共点：②三条直线两两平行；③三条直线共点；④有两条直线平行，第三条直线和这两条直线都相交．其中，使三条直线共面的充分条件有 ．

2167．已知复数z满足|z|=2，z2的虚部为2．（1）求复数z；（2）设z、z2、z-z2在复平面上的对应点分别为A、B、C，求△ABC的面积．

2168．如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=2．（Ⅰ）证明：平面A1BD∥平面CD1B1；（Ⅱ）求三棱柱ABD-A1B1D1的体积．

2170．若OA=（-1，2），OB=（1，-1），则AB=（ ）

2162．已知复数z=2+i（i是虚数单位）是关于x的实系数方程x²+px+q=0在复数范围内的一个根．
（1）求p+q的值；
（2）复数w满足z•w是实数，且|w|=2
5
，求复数w.

2163．在锐角△ABC中，角A，B，C所对的边分别为a,b,c.已知2bsinA-
3
a=0．
（Ⅰ）求角B的大小；
（Ⅱ）求cosA+cosB+cosC的取值范围．

2164．如图，在矩形ABCD中，AB=
2
，BC=2，点E为BC的中点，点F在边CD上，若
AB
•
AF
=
2
，则
AE
•
BF
的值是
．

2165．对于空间三条直线，有下列四个条件：
①三条直线两两相交且不共点：
②三条直线两两平行；
③三条直线共点；
④有两条直线平行，第三条直线和这两条直线都相交．
其中，使三条直线共面的充分条件有
．

2167．已知复数z满足
|
z
|
=
2
，z²的虚部为2．
（1）求复数z；
（2）设z、z²、z-z²在复平面上的对应点分别为A、B、C，求△ABC的面积．

2168．如图，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是正方形，O为底面中心，A₁O⊥平面ABCD，AB=AA₁=
2
．
（Ⅰ）证明：平面A₁BD∥平面CD₁B₁；
（Ⅱ）求三棱柱ABD-A₁B₁D₁的体积．

2170．若
OA
=（-1，2），
OB
=（1，-1），则
AB
=（　　）