当前位置：试卷中心 > 试卷详情

2023-2024学年陕西省咸阳市秦都区彩虹中学八年级（上）期中数学试卷

发布：2024/10/1 14:0:1

一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）

1．
1
64
的立方根是（　　）
A．
1
4
B．±
1
4
C．±
1
2
D．
1
2
组卷：228引用：10难度：0.9
解析
2．下列实数中，属于无理数的是（　　）
A．
4
3
B．
7
C．3.14 D．
4
组卷：453引用：12难度：0.9
解析
3．下列几组数据中，能作为直角三角形的三边长的是（　　）
A．2，3，4 B．
3
，
4
，
5
C．4，6，9 D．
3
，
13
，
4
组卷：16引用：1难度：0.7
解析
4．下列各组二次根式中，能进行合并的是（　　）
A．
6
和
3
B．
8
和
2
C．
12
和
2
D．
18
和
12
组卷：265引用：4难度：0.7
解析
5．定义一种新运算“△”，a△b=a²-ab,则
2
△1的值为（　　）
A．
1
-
2
B．
1
+
2
C．
2
-
2
D．
2
+
2
组卷：586引用：5难度：0.5
解析
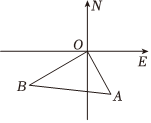6．如图，在我军某次海上演习中，两艘航母护卫舰从同一港口O同时出发，1号舰沿东偏南60°方向以9节（1节=1海里/小时）的速度航行，2号舰沿南偏西60°方向以12节的速度航行，离开港口2小时后它们分别到达A，B两点，此时两舰的距离是（　　）
A．9海里 B．12海里 C．15海里 D．30海里
组卷：885引用：6难度：0.5
解析
7．在平面直角坐标系中，点P与点A关于x轴对称，点P与点B关于y轴对称．已知点B（1，2），则点A的坐标是（　　）
A．（-1，2） B．（-1，-2） C．（-2，-1） D．（-2，1）
组卷：315引用：4难度：0.7
解析
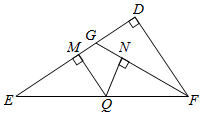8．如图，在△DEF中，∠D=90°，DG：GE=1：3，GE=GF，Q是EF上一动点，过点Q作QM⊥DE于M，QN⊥GF于N，
EF
=
4
3
，则QM+QN的长是（　　）
A．4
3
B．3
2
C．4 D．2
3
组卷：5338引用：14难度：0.3
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共13小题，计81分．解答应写出过程）

25．阅读材料：
材料一：两个含有二次根式且非零的代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式．
例如：
3
×
3
=
3
，
（
6
-
2
）
（
6
+
2
）
=
6
-
2
=
4
，我们称
3
的一个有理化因式是
3
，
6
-
2
的一个有理化因式是
6
+
2
．
材料二：如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含二次根式，这种变形叫做分母有理化．
例如：
1
3
=
1
×
3
3
×
3
=
3
3
，
8
6
-
2
=
8
（
6
+
2
）
（
6
-
2
）
（
6
+
2
）
=
8
（
6
+
2
）
4
=
2
（
6
+
2
）
．
请你仿照材料中的方法探索并解决下列问题：
（1）
13
的有理化因式为
，
7
+
5
的有理化因式为
；（均写出一个即可）
（2）将下列各式分母有理化（要求：写出变形过程）：
①
3
15
；
②
2
5
+
3
；
（3）计算：
1
1
+
2
+
1
3
+
2
+
1
3
+
4
+
⋯
+
1
2022
+
2023
的结果．
组卷：47引用：5难度：0.5
解析
26．如图，△ABC在平面直角坐标系中，点A（4，0）、B分别在x轴、y轴的正半轴上，点C在y轴的负半轴上．

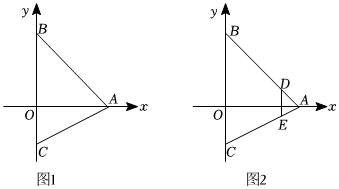
（1）如图1，已知B（0，4），C（0，-2）．
①求AB，AC的长；
②在线段AC上有一点M，当点B到点M的距离最小时，求BM的长；
（2）如图2，已知D（3，1），
E
（
3
，-
1
2
）
，点Q是线段OA上一点．当△DEQ为等腰三角形时，求点Q的坐标．
组卷：200引用：2难度：0.2
解析