阅读材料：
材料一：两个含有二次根式且非零的代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式．
例如：3×3=3，（6-2）（6+2）=6-2=4，我们称3的一个有理化因式是3，6-2的一个有理化因式是6+2．
材料二：如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含二次根式，这种变形叫做分母有理化．
例如：13=1×33×3=33，
86-2=8（6+2）（6-2）（6+2）=8（6+2）4=2（6+2）．
请你仿照材料中的方法探索并解决下列问题：
（1）13的有理化因式为 1313，7+5的有理化因式为 7-57-5；（均写出一个即可）
（2）将下列各式分母有理化（要求：写出变形过程）：
①315；
②25+3；
（3）计算：11+2+13+2+13+4+⋯+12022+2023的结果．
3
×
3
=
3
（
6
-
2
）
（
6
+
2
）
=
6
-
2
=
4
3
3
6
-
2
6
+
2
1
3
=
1
×
3
3
×
3
=
3
3
8
6
-
2
=
8
（
6
+
2
）
（
6
-
2
）
（
6
+
2
）
=
8
（
6
+
2
）
4
=
2
（
6
+
2
）
13
13
13
7
+
5
7
-
5
7
-
5
3
15
2
5
+
3
1
1
+
2
+
1
3
+
2
+
1
3
+
4
+
⋯
+
1
2022
+
2023
【答案】；
13
7
-
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/1 14:0:1组卷：47引用：5难度：0.5
相似题
-
1．观察下列顺序排列的等式：9×0+1=1，9×1+2=11，9×2+3=21，9×3+4=31，9×4+5=41，…，猜想：第20个等式应为
．发布：2025/6/18 7:30:1组卷：82引用：1难度：0.9 -
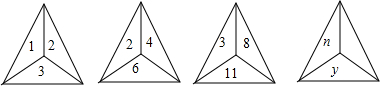
2．如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系是（ ）
发布：2025/6/18 6:30:1组卷：4111引用：44难度：0.7 -
3．观察下列算式：
①1×3-22=-1；②2×4-32=-1；③3×5-42=-1；④；
（1）请你按以上规律写出第4个算式；
（2）把这个规律用含字母的式子表示出来；
（3）你认为第（2）小题中所写出的式子一定成立吗？并说明理由．发布：2025/6/18 6:30:1组卷：148引用：4难度：0.7
