2022-2023学年江西省赣州市大余中学高一（下）期中数学试卷

一、单选题（每题5分，共40分）

• 1．下列说法正确的是（　　）

  A．零向量是没有方向的向量

  B．零向量的长度为0

  C．任意两个单位向量的方向相同

  D．同向的两个向量可以比较大小
  组卷：627引用：3难度：0.9

  解析

• 2．设

  θ

  ∈

  （

  0

  ，

  π

  2

  ）

  ，则sinθ+cosθ的一个可能值是（　　）

  A．2

  B．1

  C． 2 3

  D． π 3
  组卷：134引用：3难度：0.7

  解析

• 3．

  a

  =

  （

  1

  ，-

  2

  ）

  ，

  b

  =

  （

  -

  3

  ，

  5

  ）

  ，

  c

  =

  （

  1

  ，

  2

  ）

  ，则

  （

  2

  a

  +

  b

  ）

  •

  c

  =（　　）

  A．1

  B．-1

  C．3

  D．（-1，2）
  组卷：74引用：1难度：0.8

  解析

• 4．已知函数f（x）=g（x）cos（x+

  π

  4

  ），若函数f（x）是最小正周期为π的偶函数，则g（x）可以是（　　）

  A．cosx

  B．sinx

  C．cos（x+ π 4 ）

  D．sin（x+ π 4 ）
  组卷：298引用：2难度：0.7

  解析

• 5．下列化简结果正确的个数为（　　）
  ①

  cos

  22

  °

  sin

  52

  °

  -

  sin

  22

  °

  cos

  52

  °=

  1

  2

  ；
  ②

  tan

  24

  °

  +

  tan

  36

  °

  1

  -

  tan

  24

  °

  tan

  36

  °

  =

  3

  ；
  ③

  cos

  15

  °

  -

  sin

  15

  °=

  2

  2

  ；
  ④

  sin

  15

  °

  sin

  30

  °

  sin

  75

  °=

  1

  4

  ．

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：166引用：3难度：0.7

  解析

• 6．关于△ABC给出下列命题：
  ①若sinA=2sinBcosC，则该三角形为等腰三角形；
  ②若sin2A=sin2B，则△ABC是等腰三角形；
  ③若sinA=cosB，则△ABC是直角三角形；
  ④在△ABC中，恒有cosAcosBcosC＜sinAsinBsinC；
  ⑤若cos（A-B）cos（B-C）cos（C-A）=1，则△ABC是等边三角形．
  其中正确命题的个数是（　　）

  A．2个

  B．3个

  C．4个

  D．5个
  组卷：63引用：4难度：0.6

  解析

• 7．已知函数y=sin（ωx+φ）的两条相邻的对称轴的间距为

  π

  2

  ，现将y=sin（ωx+φ）的图象向左平移

  π

  8

  个单位后得到一个偶函数，则φ的一个可能取值为（　　）

  A． 3 π 4

  B． π 4

  C．0

  D． - π 4
  组卷：606引用：3难度：0.7

  解析

四、解答题（共70分）

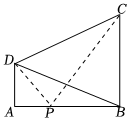• 21．如图，为了测量某条河流两岸两座高塔底部A，B之间的距离，观测者在其中一座高塔的顶部D测得另一座高塔底部B和顶部C的视角为45°（即∠BDC=45°），已知两座高塔的高AD为30m,BC为75m,塔底A，B在同一水平面上，且AD⊥AB，BC⊥AB．
  （1）求两座高塔底部A，B之间的距离；
  （2）为庆祝2023年春节的到来，在两座高塔顶部各安装了一个大型彩色灯饰．政府部门为了方便市民观赏这两个彩色灯饰，决定在A，B之间的点P处（点P在线段AB上）搭建一个水上观景台，为了达到最佳的观赏效果，要求∠DPC最大，问：在距离A点多远处搭建，才能达到最佳的观赏效果？
  组卷：47引用：4难度：0.4

  解析

• 22．已知函数f（x）=-cos²x+2acosx+a²+2（x∈R）．
  （1）若函数f（x）的最大值是最小值的4倍，求实数a的值；
  （2）若函数f（x）存在零点，求函数的零点．
  组卷：48引用：1难度：0.5

  解析