2022-2023学年重庆一中高一（下）第一次月考数学试卷（3月份）

一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知a∈R，（1+ai）i=3+i（i为虚数单位），则a=（　　）

  A．-1

  B．1

  C．-3

  D．3
  组卷：2613引用：20难度：0.9

  解析

• 2．已知矩形ABCD中，

  AE

  =

  EB

  ，线段AC和DE交于点F，则

  BF

  =（　　）

  A． - 1 3 AB + 2 3 AD

  B． 1 3 AB - 2 3 AD

  C． 2 3 AB - 1 3 AD

  D． - 2 3 AB + 1 3 AD
  组卷：174引用：1难度：0.7

  解析

• 3．若向量

  a

  ，

  b

  满足|

  a

  |=

  2

  ，|

  b

  |=2，

  a

  ⊥（

  a

  -

  b

  ），则

  a

  与

  b

  的夹角为（　　）

  A． π 4

  B． π 3

  C． 2 π 3

  D． 3 π 4
  组卷：288引用：4难度：0.8

  解析

• 4．将函数

  f

  （

  x

  ）

  =

  3

  sin

  2

  x

  -

  2

  co

  s

  2

  x

  图象上各点的横坐标伸长到原来的3倍（纵坐标不变），再向右平移

  π

  8

  个单位长度，则所得函数图象的一个对称中心为（　　）

  A． （ 3 π 8 ， 0 ）

  B．（- 3 π 8 ，-1）

  C． （ - 3 π 8 ， 0 ）

  D．（ 3 π 8 ，-1）
  组卷：237引用：5难度：0.8

  解析

• 5．已知

  a

  =

  （

  sinα

  ，

  1

  -

  4

  cos

  2

  α

  ）

  ，

  b

  =

  （

  1

  ，

  3

  sinα

  -

  2

  ）

  ，

  α

  ∈

  （

  0

  ，

  π

  2

  ）

  ，若

  a

  ∥

  b

  ，则

  sin

  2

  α

  2

  +

  cos

  2

  α

  =（　　）

  A． 2 11

  B． 4 11

  C． 6 11

  D． 8 11
  组卷：203引用：6难度：0.7

  解析

• 6．设A₁、A₂、A₃、A₄为平面直角坐标系中两两不同的点，若

  A

  1

  A

  3

  =

  λ

  A

  1

  A

  2

  （

  λ

  ∈

  R

  ）

  ，

  A

  1

  A

  4

  =

  μ

  A

  1

  A

  2

  （

  μ

  ∈

  R

  ）

  ，且

  1

  λ

  +

  1

  μ

  =

  4

  ，则称点A₃、A₄和谐分割点A₁、A₂.已知平面上两两不同的点A、B、C、D，若C、D和谐分割点A、B．则下面说法正确的是（　　）

  A．点C可能是线段AB的中点

  B．点C可能是靠近点A的线段AB的三等分点

  C．点C、D可能同时在线段AB上

  D．点C、D可能同时在线段AB的延长线上
  组卷：128引用：3难度：0.5

  解析

• 7．在△ABC中，角A，B，C的对边分别为a,b,c,已知（sinA+sinB）（a-b）=sinC（b+c），若角A的内角平分线AD的长为3，则b+c的最小值为（　　）

  A．12

  B．24

  C．27

  D．36
  组卷：503引用：6难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

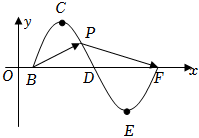• 21．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象如图所示，点B，D，F为f（x）与x轴的交点，点C，E分别为f（x）的最高点和最低点，而函数f（x）的相邻两条对称轴之间的距离为2，且其在

  x

  =

  -

  1

  2

  处取得最小值．
  （1）求参数ω和φ的值；
  （2）若A=1，求向量

  2

  BC

  -

  CD

  与向量

  BC

  +

  3

  CD

  夹角的余弦值；
  （3）若点P为函数f（x）图象上的动点，当点P在C，E之间运动时，

  BP

  •

  PF

  ≥1恒成立，求A的取值范围．
  组卷：427引用：11难度：0.3

  解析

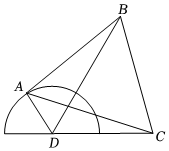• 22．为提升城市旅游景观面貌，城建部门拟对一公园进行改造，已知原公园是直径为200米的半圆，出入口在圆心D处，C点为一居民小区，CD距离为200米，按照设计要求，取圆弧上一点A，并以线段AC为一边向圆外作等边三角形ABC，使改造之后的公园成四边形ABCD，并将△BCD区域建成免费开放的植物园，如图所示．
  （1）若DA⊥DC时，点B与出入口D的距离为多少米？
  （2）A设计在什么位置时，免费开放的植物园区域△BCD面积最大？并求此最大面积．
  组卷：106引用：3难度：0.4

  解析